练习册

  • 练习册
  • 试题
    在学习无理数时.要花简一个分母含有根式的式子.我们常常进行分母有理化.如= 【查看更多】

     

    题目列表(包括答案和解析)

    某电视台在因特网上就观众对其某一节目的喜爱程度进行调查，参加调查的人数为20000人，其中持各种态度的人数如下表所示：
    最喜爱 喜爱 一般 不喜欢
    4817 7188 6392 1603
    电视台为了了解观众的具体想法和意见，打算从中抽选出100人进行更为详细的调查，为此要进行分层抽样，那么在分层抽样时，每类人中各应抽选出的人数近似为（　　）
    A、25，25，25，25
    B、48，72，64，16
    C、20，40，30，10
    D、24，36，32，8

    查看答案和解析>>

    （2013•上海）如图，已知双曲线C1：
    x2
    2
    -y2=1    ，曲线C2：|y|=|x|+1，P是平面内一点，若存在过点P的直线与C1，C2都有公共点，则称P为“C1-C2型点”
    （1）在正确证明C1的左焦点是“C1-C2型点“时，要使用一条过该焦点的直线，试写出一条这样的直线的方程（不要求验证）；
    （2）设直线y=kx与C2有公共点，求证|k|＞1，进而证明原点不是“C1-C2型点”；
    （3）求证：圆x2+y2=
    1
    2
    内的点都不是“C1-C2型点”

    查看答案和解析>>

    如图，已知双曲线C1:，曲线C2:.P是平面内一点.若存在过点P的直线与C1、C2都有共同点，则称P为“C1-C2型点”.

    （1）在正确证明C1的左焦点是“C1-C2型点”时，要使用一条过该焦点的直线，试写出一条这样的直线的方程（不要求验证）；

    （2）设直线y=kx与C2有公共点，求证＞1，进而证明圆点不是“C1-C2型点”；

    （3）求证：圆内的点都不是“C1-C2型点”.

    查看答案和解析>>

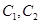    如图，已知曲线，曲线，P是平面上一点，若存在过点P的直线与都有公共点，则称P为“C1—C2型点”．

    (1)在正确证明的左焦点是“C1—C2型点”时，要使用一条过该焦点的直线，试写出一条这样的直线的方程（不要求验证）；

    (2)设直线与有公共点，求证，进而证明原点不是“C1—C2型点”；

    (3)求证：圆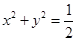内的点都不是“C1—C2型点”．

     

    查看答案和解析>>

    某工人师傅欲用系统抽样的方法从1 503个机器零件（编号为0001—1 503）中抽取35个零件，在确定分段时，要使分段的间隔数量大，则至少应从总体中剔除的个数是____________，此时分段的间隔数是____________.

    查看答案和解析>>


    同步练习册答案