光滑绝缘细杆与水平成θ角固定，杆上套有一带正电小球。为使小球静止在杆上，可加一匀强电场。问图中给出的四个方向中，沿哪些方向加电场，有可能使小球在杆上保持静止（   ）

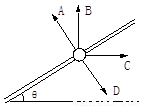Ａ．垂直于杆斜向上    

Ｂ．竖直向上   

Ｃ．水平向右         

Ｄ．垂直于杆斜向下

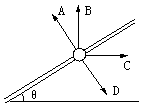
光滑绝缘细杆与水平成θ角固定，杆上套有一带正电小球。为使小球静止在杆上，可加一匀强电场。问图中给出的四个方向中，沿哪些方向加电场，有可能使小球在杆上保持静止（   ）

Ａ．垂直于杆斜向上    

Ｂ．竖直向上    

Ｃ．水平向右         

Ｄ．垂直于杆斜向下

光滑绝缘细杆与水平成θ角固定，杆上套有一带正电小球。为使小球静止在杆上，可加一匀强电场。问图中给出的四个方向中，沿哪些方向加电场，有可能使小球在杆上保持静止（   ）

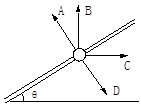Ａ．垂直于杆斜向上    

Ｂ．竖直向上   

Ｃ．水平向右         

Ｄ．垂直于杆斜向下

正负电子对撞机的最后部分的简化示意图如图甲所示（俯视图），位于水平面内的粗实线所示的圆环形真空管道是正、负电子做圆运动的“容器”，经过加速器加速后的正、负电子被分别引入该管道时，具有相等的速率ｖ，它们沿着管道向相反的方向运动．在管道内控制它们转弯的是一系列圆形电磁铁，即图中的Ａ_１、Ａ_２、Ａ_３……Ａ_ｎ共有ｎ个，均匀分布在整个圆环上，每个电磁铁内的磁场都是磁感应强度相同的匀强磁场，并且方向竖直向下，磁场区域的直径为ｄ，改变电磁铁内电流的大小，就可改变磁场的磁感应强度，从而改变电子偏转的角度．经过精确的调整，首先实现电子在环形管道中沿图甲中粗虚线所示的轨迹运动，这时电子经过每个电磁场区域时射入点和射出点都是电磁场区域的同一条直径的两端，如图乙所示．这就为进一步实现正、负电子的对撞作好了准备．

（1）试确定正、负电子在管道内各是沿什么方向旋转的；

（2）已知正、负电子的质量都是ｍ，所带电荷都是元电荷ｅ，重力可不计，求电磁铁内匀强磁场的磁感应强度Ｂ的大小．