查看答案和解析>>

（坐标系与参数方程）两直线与的位置关系是：    （判断垂直或平行或斜交）

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

已知点P是直角坐标平面内的动点，点P到直线l₁：x=-2的距离为d₁，到点F（-1，0）的距离为d₂，且．
（1）求动点P所在曲线C的方程；
（2）直线l过点F且与曲线C交于不同两点A、B（点A或B不在x轴上），分别过A、B点作直线l₁：x=-2的垂线，对应的垂足分别为M、N，试判断点F与以线段MN为直径的圆的位置关系（指在圆内、圆上、圆外等情况）；
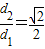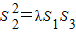（3）记S₁=S_△FAM，S₂=S_△FMN，S₃=S_△FBN（A、B、M、N是（2）中的点），问是否存在实数λ，使成立．若存在，求出λ的值；若不存在，请说明理由．

查看答案和解析>>

1-15CBDAC CDB   0   5   100  [3.9]   垂直  2或8  

16.⑴ ∵ ，……………………………… 2分

又∵ ，∴ 而为斜三角形，

∵，∴.   ……………………………………………………………… 4分

∵，∴ .  …………………………………………………… 6分

⑵∵，∴ …10分

即，∵，∴.…………………………………12分

17.（Ⅰ）从4名运动员中任取两名，其靶位号与参赛号相同，有种方法，另2名运动员靶位号与参赛号均不相同的方法有1种，所以恰有一名运动员所抽靶位号与参赛号相同的概率为  _{……………………………4分}

   （Ⅱ）①由表可知，两人各射击一次，都未击中9环的概率为P=（1-0.3）（1-0.32）=0.476至少有一人命中9环的概率为p=1-0.476=0.524………………………8分

②   

所以2号射箭运动员的射箭水平高…………………………………12分

18.证明:（Ⅰ）在梯形ABCD中，∵，

∴四边形ABCD是等腰梯形，

且

∴，∴

又∵平面平面ABCD，交线为AC，∴平面ACFE…………………6分

（Ⅱ）取EF中点G，EB中点H，连结DG、GH、DH，∵DE=DF，∴ ∵平面ACFE，∴  又∵，∴又∵，∴

∴是二面角B―EF―D的平面角.

在△BDE中∴

∴，∴又∴在△DGH中，

由余弦定理得即二面角B―EF―D的大小余弦值...14分

19.解：（1）由椭圆定义可得，可得

而,,解得   （4分）

（或解：以为直径的圆必与椭圆有交点，即

   （2）由，得

解得    

    此时

当且仅当m=2时， （9分）

（3）由

设A，B两点的坐标分别为，中点Q的坐标为

则，两式相减得

     ①

且在椭圆内的部分

又由可知

    ②

①②两式联立可求得点Q的坐标为

点Q必在椭圆内

 又             _(14分)

20.解：（1）

故_{……………………………4分}

(2)

故

由此猜测

下面证明：当时，由

得

若

当

当时,

当时，

总之故在(-                （10分）

又

所以当时，在（-1，0）上有唯一实数解，从而在

上有唯一实数解。

综上可知，.                 (14分)

21.解：（1）令

   令

   由①②得           （6分）

  （2）由（1）可得

则

又

_n     

又

      _{………………14分}