题目列表(包括答案和解析)
（14分）已知椭圆
的中心在原点，焦点在
轴上，离心率为
，且椭圆经过圆C： 
的圆心C。
（Ⅰ）求椭圆的方程；
（Ⅱ） 设
是椭圆上的一点，过点的直线
交轴于点
，交
轴于点
，若
，求直线的斜率．
已知椭圆
的中心在原点
，焦点在
轴上，右准线的方程为
，倾斜角为
的直线
交椭圆于
两点，且
的中点坐标为
，设
为椭圆的右顶点，
为椭圆上两点，且
，
，
三者的平方成等差数列，则直线
和
斜率之积的绝对值是否为定值，若是，请求出定值；若不是，请说明理由．
已知椭圆
的中心在原点，焦点在
轴上，椭圆上的点到焦点的距离的最小值为
，离心率为
．
（1）求椭圆的方程；
（2）过点
作直线
交于
、
两点，试问：在轴上是否存在一个定点
，使
为定值？若存在，求出这个定点的坐标；若不存在，请说明理由．
已知椭圆
的中心在原点
，焦点在
轴上，右准线的方程为
，倾斜角为
的直线
交椭圆于
两点，且
的中点坐标为
，求椭圆的方程；
已知椭圆
的中心在原点，焦点在
轴上，以两个焦点和短轴的两个端点为顶点的四边形是一个面积为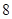
的正方形（记为
）
（Ⅰ）求椭圆的方程
（Ⅱ）设点
是直线
与轴的交点，过点的直线
与椭圆相交于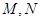
两点，当线段
的中点落在正方形内（包括边界）时，求直线斜率的取值范围
一、选择题：
1．D 2． B 3．B 4．A 5．C 6．D 7．C 8．C 9．D 10．D
二、填空题：
11．3 12．
13．1 14．
15．1005 16．①③④
三、解答题：
17．解：（本小题满分12分）
解：（I）
……………………2分
由
解得
…………………………5分
（II）解：由
-----------7分
------------------9分
-----------------12分
18．（本小题满分12分）
解: （Ⅰ）这5天的平均发芽率为
……5分
（Ⅱ）
的取值情况有
，
,
．基本事件总数为10．
……8分
设“
”为事件
，则事件包含的基本事件为
……9分
所以
，
故事件“”的概率为
．
……12分
19．（本小题满分12分）
（Ⅰ）记
与
的交点为
，
则
，---------------1分
连接
，
且
，
所以
则四边形
是平行四边形，
-------------------------------2分
则
，又
面ACE，
面ACE，故BF∥平面ACE； -----------------------------4分
（Ⅲ）（方法1）设点
到平面
的距离为
，由于
，且
平面
所以
，
--------------------------10分
又
，
，
所以
-----------------------12分
（方法2）点到平面的距离等于点
到平面的距离， ----------------9分
也等于点
到平面的距离，
-------------------------10分
该距离就是
斜边上的高，即
．-------------------12分
20．（本小题满分12分）
（Ⅰ）
------------------------3分
（Ⅱ）因第i行的第一个数是
，
∴
＝
．
∵
，
，
∴
．
------------------------6分
令
,
解得
．
------------------------8分
（Ⅲ）∵
------------------------9分
．
-----------------12分
21． （本小题满分14分）
解：（Ⅰ）圆C方程化为：
，
圆心C
………………………………1分
设椭圆的方程为
，……………………………………．．2分
则 
……………………………．．5分
所以所求的椭圆的方程是：
…………………………………………．6分
（Ⅱ）由题意可知直线
的斜率存在，设直线斜率为
，则直线的方程为
，则有
．……………………………………．．7分
设
，由于
、、
三点共线，且
．
根据题意得
,
…………9分
解得
或
．
…………11分
又在椭圆上，故
或
， …………12分
解得
,
所以直线的斜率为
或
…………14分
22．（本小题满分14分）
解：（Ⅰ）当
时，
，
；………………2分
对于
[1，e]，有
，∴
在区间[1，e]上为增函数，…………3分
∴
，
．……………………………5分
（Ⅱ）令
，
则
的定义域为（0，+∞）．…………………………………6分
在区间（1，+∞）上，
函数的图象恒在直线
下方等价于
在区间
（1，+∞）上恒成立．
② 若
，则有
，此时在区间(1，+∞)上恒有
，
从而在区间(1，+∞)上是减函数；……………………………………12分
要使在此区间上恒成立，只须满足
，
由此求得
的范围是[
，
]．
综合①②可知，当∈[，]时，函数的图象恒在直线下方．
………………………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com