
题目列表(包括答案和解析)
| 人名编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 年收入(万元) | 15 | 5 | 7 | 16 | 14 | 3 | 4 | 6 | 20 | 8 | 4 | 12 | 5 | 6 | 4 | 30 | 3 | 7 | 4 | 6 |
| 购房数量(套) | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 高收入 | 普通收入 | 合计 | |
| 已购房 | |||
| 未购房 | |||
| 合计 | 20 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(本小题满分13分)已知A,B分别是直线y=x和y=-x上的两个动点,线段AB的长为2 ,D是AB的中点.
,D是AB的中点.
(1)求动点D的轨迹C的方程;
(2)若过点(1,0)的直线l与曲线C交于不同两点P、Q,
①当|PQ|=3时,求直线l的方程;
②设点E(m,0)是x轴上一点,求当 ·
· 恒为定值时E点的坐标及定值.
恒为定值时E点的坐标及定值.
已知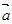 =(3,1),
=(3,1), =(
=(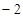 ,5)则3
,5)则3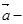 2
2 =
( )
=
( )
A.(2,7)
B.(13,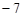 ) C.(2,
) C.(2,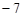 ) D.(13,13)
) D.(13,13)
(本题满分13分)
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B在AM上,D在AN上,对角线MN过C点,已知|AB|=3米,|AD|=2米,且受地理条件限制,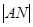 长不超过
长不超过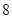 米。
米。

(1)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(2)若|AN| 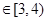 (单位:米),则当AM、AN的长度是多少时,矩形花坛AMPN的面积最大?并求出最大面积.
(单位:米),则当AM、AN的长度是多少时,矩形花坛AMPN的面积最大?并求出最大面积.
 长不超过
长不超过 米。
米。
 (单位:米),则当AM、AN的长度是多少时,矩形花坛AMPN的面积最大?并求出最大面积.
(单位:米),则当AM、AN的长度是多少时,矩形花坛AMPN的面积最大?并求出最大面积.
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
B
C
C
B
C
D
A
D
A
B
二、填空题
13.24 14. .files/image131.gif) 15.
15. .files/image133.gif) 16. ①④
16. ①④
三、解答题
17. 解:(Ⅰ)因为各组的频率和等于1,故第四组的频率:
.files/image135.gif)
.files/image137.gif) ……4分
……4分
直方图如右所示……………
(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组,
频率和为 .files/image139.gif)
所以,抽样学生成绩的合格率是.files/image141.gif) %..........................6分
%..........................6分
(Ⅲ).files/image143.gif) ,
,.files/image145.gif) ,
,.files/image147.gif) ,
,.files/image149.gif) ”的人数是9,18,15,3。所以从成绩是60分以上(包括60分)的学生中选一人,该生是优秀学生的概率是
”的人数是9,18,15,3。所以从成绩是60分以上(包括60分)的学生中选一人,该生是优秀学生的概率是
.files/image151.gif) ……………………………………………………10分
……………………………………………………10分
18.(Ⅰ)证法一:取.files/image153.gif) 的中点G,连结FG、AG,
的中点G,连结FG、AG,
依题意可知:GF是.files/image155.gif) 的中位线,
的中位线,
则 GF∥.files/image157.gif) 且
且.files/image159.gif) ,
,
AE∥.files/image157.gif) 且
且.files/image161.gif) ,
,
所以GF∥AE,且GF=AE,即四边形AEFG为平行四边形,………3分
则EF∥AG,又AG.files/image163.gif) 平面
平面.files/image165.gif) ,EF
,EF.files/image167.gif) 平面
平面.files/image165.gif) ,
,
所以EF∥平面.files/image165.gif) .
………6分
.
………6分
证法二:取DC的中点G,连结FG,GE.
∵.files/image169.gif) ∥
∥.files/image153.gif) ,
,.files/image172.gif) 平面
平面.files/image165.gif) , GF
, GF.files/image167.gif) 平面
平面.files/image165.gif) ∴FG∥平面
∴FG∥平面.files/image165.gif) .………3分
.………3分
同理:.files/image175.gif) ∥平面
∥平面.files/image165.gif) ,且
,且.files/image177.gif) ,∴平面EFG∥平面
,∴平面EFG∥平面.files/image165.gif) ,
,.files/image179.gif) 平面
平面.files/image181.gif) ,
,
∴EF∥平面.files/image165.gif) .
………6分
.
………6分
证法三:连结EC延长交AD于K,连结.files/image183.gif) , E、F分别CK、CD1的中点,
, E、F分别CK、CD1的中点,
所以 FE∥D1K ……3分
.files/image185.gif) ∵FE∥D1K,
∵FE∥D1K,.files/image187.gif) 平面
平面.files/image165.gif) ,
, .files/image189.gif)
.files/image167.gif) 平面
平面.files/image165.gif) ,∴EF∥平面
,∴EF∥平面.files/image165.gif) .………6分
.………6分
(Ⅱ)解:.files/image192.gif)
.files/image194.gif)
.files/image196.gif) .
.
.files/image198.gif)
.files/image200.gif) .
.
∴.files/image202.gif) 的值为1. ………12分
的值为1. ………12分
19.解:(1).files/image204.gif)
.files/image206.gif) ………3分
………3分
∵角A为钝角,
.files/image208.gif) ………………4分
………………4分
.files/image210.gif) 取值最小值,
取值最小值,
其最小值为.files/image212.gif) ……………………6分
……………………6分
(2)由.files/image214.gif) ………………8分
………………8分
.files/image216.gif) ,
,
.files/image218.gif) …………10分
…………10分
在△.files/image220.gif) 中,由正弦定理得:
中,由正弦定理得:.files/image222.gif) ……12分
……12分
20.解:(1).files/image224.gif)
由题意得.files/image226.gif) ,经检验满足条件。 …………2分
,经检验满足条件。 …………2分
(2)由(1)知.files/image228.gif) …………4分
…………4分
令.files/image230.gif) (舍去)…
……………6分
(舍去)…
……………6分
当x变化时,.files/image232.gif) 的变化情况如下表:
的变化情况如下表:
x
-1
(-1,0)
0
(0,1)
1
.files/image234.gif)
-
0
+
.files/image009.gif)
-1
ㄋ
-4
ㄊ
-3
……………9分
∵关于x的方程.files/image237.gif) 上恰有两个不同的实数根,
上恰有两个不同的实数根,
.files/image239.gif) …………12分
…………12分
21.解:⑴设动点的坐标为P(x,y),则.files/image241.gif) =(x,y-2),
=(x,y-2),.files/image243.gif) =(x,y+2),
=(x,y+2),.files/image245.gif) =(2-x,-y)
=(2-x,-y)
∵.files/image241.gif) ?
?.files/image243.gif) =m|
=m|.files/image245.gif) |2,
|2,
∴x2+y2-4=m[(x-2)2+y2]
即(1-m)x2+(1-m)y2+4mx-
若m=1,则方程为x=2,表示过点(2,0)且平行于y轴的直线; ………4分
若m≠1,则方程化为:.files/image248.gif) ,表示以(
,表示以(.files/image250.gif) ,0)为圆心,以
,0)为圆心,以.files/image252.gif) 为半径的圆;
………6分
为半径的圆;
………6分
(2)当m=2时,方程化为(x-4)2+y2=4;
设.files/image254.gif) ,则
,则.files/image256.gif) ,圆心到直线距离
,圆心到直线距离.files/image258.gif) 时,………8分
时,………8分
解得.files/image260.gif) ,又
,又.files/image117.gif) ,所以图形为上半个圆(包括与
,所以图形为上半个圆(包括与.files/image263.gif) 轴的两个交点)……10分
轴的两个交点)……10分
故直线与半圆相切时.files/image265.gif) ;
;
当直线过.files/image263.gif) 轴上的两个交点时知
轴上的两个交点时知.files/image267.gif) ;
;
因此.files/image269.gif) 的取值范围是
的取值范围是.files/image271.gif) .
………12分
.
………12分
22.解:(1)
.files/image273.gif)
2
3
51
200
.files/image275.gif)
196
192
1
4
………4分
(2).files/image277.gif) 由题意知数列
由题意知数列.files/image279.gif) 的前50项成首项为200,公差为-4的等差数列,从第51项开始,奇数项均为1,偶数项均为4.
的前50项成首项为200,公差为-4的等差数列,从第51项开始,奇数项均为1,偶数项均为4.
从而.files/image281.gif) =
=.files/image283.gif)
=.files/image285.gif) .
……………6分
.
……………6分
(3)当.files/image287.gif) 时,因为
时,因为.files/image289.gif) ,
,
所以.files/image291.gif) …………8分
…………8分
当.files/image293.gif) 时,
时,
.files/image295.gif)
.files/image297.gif)
.files/image299.gif)
因为.files/image287.gif) ,所以
,所以.files/image302.gif) , ……………10分
, ……………10分
当.files/image304.gif) 时,
时,
.files/image306.gif)
综上:.files/image308.gif) .
……………12分
.
……………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com