题目列表(包括答案和解析)
如图，P是椭圆
＝1上的一点，F是椭圆的左焦点，且
＝
(
＋
)，||＝4，则点P到该椭圆左准线的距离为
A．6
B．4
C．3
D．
如图，F是椭圆
＝1(a＞b＞0)的一个焦点，A、B是椭圆的两个顶点，椭圆的离心率为
，点C在x轴上，BC⊥BD，B，C，F三点确定的圆M恰好与直线x＋
y＋3＝0相切．
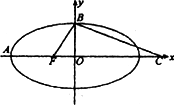
(Ⅰ)求椭圆的方程；
(Ⅱ)过F作一条与两坐标轴都不垂直的直线l交椭圆于P、Q两点，在x轴上是否存在点N，使得NF恰好为△PNQ的内角平分线，若存在，求出点N的坐标，若不存在，请说明理由．
如图，F是椭圆
＝1(a＞b＞0)的一个焦点，A、B是椭圆的两个顶点，椭圆的离心率为
，点C在x轴上，BC⊥BF，B，C，F三点确定的圆M恰好与直线x＋
y＋3＝0相切．
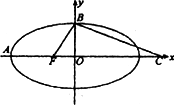
(Ⅰ)求椭圆的方程；
(Ⅱ)过F作一条与两坐标轴都不垂直的直线l交椭圆于P、Q两点，在x轴上是否存在点N，使得NF恰好为△PNQ的内角平分线，若存在，求出点N的坐标，若不存在，请说明理由．
如图，正方形ABCD内接于椭圆
＝1(a＞b＞0)，且它的四条边与坐标轴平行，正方形MNPQ的顶点M、N在椭圆上，顶点P、Q在正方形的边AB上，且A、M都在第一象限．
(1)若正方形ABCD的边长为4，且与y轴交于E、F两点，正方形MNPQ的边长为2.
①求证：直线AM与△ABE的外接圆相切；
②求椭圆的标准方程；
(2)设椭圆的离心率为e，直线AM的斜率为k，求证：2e2－k是定值．
＝1(a＞b＞0)，且它的四条边与坐标轴平行，正方形MNPQ的顶点M、N在椭圆上，顶点P、Q在正方形的边AB上，且A、M都在第一象限．
一、ABBDA CCDBC DD
二、13、6； 14、x2＋(y－3)2＝1； 15、－8； 16、①③
三、17.(1)f(x)＝2sin(2x＋),T＝π (2)x＝或
18.(1)；(2)Eξ＝1.5 19.(1)；(2)arccos；(3)a
20.(1)a1＝5；a2＝13；a3＝33；(2)λ＝－1；(3)Sn＝n(2n＋1＋1)
21.(1)略；(2)a∈(－∞,3] 22.(1)y＝±x；(2) ＝1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com