
题目列表(包括答案和解析)
(06年福建卷文)(12分)
已知![]() 是二次函数,不等式
是二次函数,不等式![]() 的解集是
的解集是![]() 且
且![]() 在区间
在区间![]() 上的最大值是12。
上的最大值是12。
(I)求![]() 的解析式;
的解析式;
(II)是否存在实数![]() 使得方程
使得方程![]() 在区间
在区间![]() 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出![]() 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
(09年湖北百所重点联考文)(12分)
已知函数![]() 处的切线方程是
处的切线方程是![]()
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调递增区间。
的单调递增区间。
(08年中卫一中三模文) 给出下列四个命题:
①命题“![]() ”的否定是“
”的否定是“![]() ”;
”;
②线性相关系数r的绝对值越接近于1,表明两个随机变量线性相关性越强;
③设![]() 是方程
是方程![]() 的解,则
的解,则![]() 属于区间(1,2)
属于区间(1,2)
④若![]() 的展开式中
的展开式中![]() 的系数是80,则实数
的系数是80,则实数![]() 的值是2
的值是2
其中真命题的序号是 。(填上所有真命题的序号)
三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6个大题,共76分)。
17.(12分)以下资料是一位销售经理收集来的每年销售额和销售经验年数的关系:
|
销售经验(年) |
1 |
3 |
4 |
4 |
6 |
8 |
10 |
10 |
11 |
13 |
|
年销售额(千元) |
80 |
97 |
92 |
102 |
103 |
111 |
119 |
123 |
117 |
136 |
(1)依据这些数据画出散点图并作直线 =78+4.2x,计算
=78+4.2x,计算 (yi-
(yi- i)2;
i)2;
(2)依据这些数据由最小二乘法求线性回归方程,并据此计算 ;
;
(3)比较(1)和(2)中的残差平方和 的大小.
的大小.
三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6个大题,共76分)。
17.(12分)以下资料是一位销售经理收集来的每年销售额和销售经验年数的关系:
| 销售经验(年) | 1 | 3 | 4 | 4 | 6 | 8 | 10 | 10 | 11 | 13 |
| 年销售额(千元) | 80 | 97 | 92 | 102 | 103 | 111 | 119 | 123 | 117 | 136 |
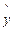 =78+4.2x,计算
=78+4.2x,计算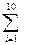 (yi-
(yi-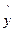 i)2;
i)2; 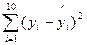 ;
;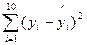 的大小.
的大小.一、 填空题(48分)
1、4 2、(理)20(文) 3、
3、 4、
4、 5、
5、 6、
6、 7、(理)
7、(理) (文)4 8、6 9、
(文)4 8、6 9、 10、
10、 11、如
11、如 12、
12、
二、 选择题(16分)
13、B 14、B 15、C 16、A
三、 解答题(86分)
17、(12分)(1) ,则
,则 ……………………… (6分)
……………………… (6分)
(2) ………………………………………(9分)
………………………………………(9分)

 …………………………………………………………(12分)
…………………………………………………………(12分)
18、(12分)(1)它是有一条侧棱垂直于底面的四棱锥

…………………………………………………………(6分)
(注:评分注意实线、虚线;垂直关系;长度比例等)
(2)由题意, ,则
,则 ,
,
 ,
,
∴需要3个这样的几何体可以拼成一个棱长为6的正方体 …(12分)
…(12分)
19、(14分)
(1)抛物线的焦点为(1,0) ……………………………………………………(2分)
设椭圆方程为 ,则
,则
∴椭圆方程为 ……………………………………………(6分)
……………………………………………(6分)
(2)设 ,则
,则

 ………………(8分)
………………(8分)
① 当 时,
时, ,即
,即 时,
时, ;
;
② 当 时,
时, ,即
,即 时,
时, ;
;
综上, 。……………………………………(14分)
。……………………………………(14分)
(注:也可设 解答,参照以上解答相应评分)
解答,参照以上解答相应评分)
20、(14分)
(1)设当天的旅游收入为L,由 得
得
 ……………………………(2分)
……………………………(2分)
由 ,知
,知 …………………………………………(4分)
…………………………………………(4分)
 ,
, 得
得 。
。
即当天的旅游收入是20万到60万。……………………………………………(7分)
(2)则每天的旅游收入上缴税收后不低于220000元
由 (
( )得
)得 ;
;
由 (
( )得
)得 ;
;
∴ ………………………………………………………………………(11分)
………………………………………………………………………(11分)
代入可得 ∴
∴
即每天游客应不少于1540人。……………………………………………………(14分)
21、(16分)
(1) 由 ,得
,得 则
则 故
故 (4分)
(4分)
(2) 由 ,得
,得 即
即
∴ ,所以
,所以 是不唯一的。……………………………………(10分)
是不唯一的。……………………………………(10分)
(3) ,
, ,
, ;
;
∴ …………………………………………(12分)
…………………………………………(12分)
(文)………………………………………………………………………………(16分)
(理)一般地,对任意复数 ,有
,有 。
。
证明:设 ,
,

 ,
,

∴ 。…………………………………………………(16分)
。…………………………………………………(16分)
22、(18分)
(1) ………………………………………………………………(6分)
………………………………………………………………(6分)
(2)由 解得
解得
即
解得 …………………………………(12分)
…………………………………(12分)
(3) 由 ,
,
又 ,
,
当 时,
时, ,
, ,
,
∴对于 时,
时, ,命题成立。………………(14分)
,命题成立。………………(14分)
以下用数学归纳法证明 对
对 ,且
,且 时,都有
时,都有 成立
成立
假设 时命题成立,即
时命题成立,即 ,
,
那么 即
即 时,命题也成立。
时,命题也成立。
∴存在满足条件的区间 。………………………………(18分)
。………………………………(18分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com