
题目列表(包括答案和解析)

如图,在□ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA.
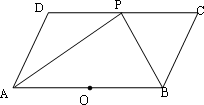
(1)判断△APB是什么三角形,证明你的结论;
(2)比较DP与PC的大小;
(3)画出以AB为直径的⊙O,交AD于点E,连结BE与AP交于点F,若AD=5 cm,AP=8 cm,求证△AEF∽△APB,并求tan∠AFE的值.
如图(1),在□ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA。
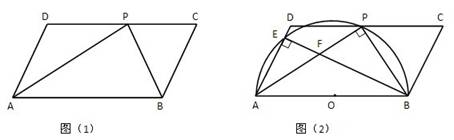
1.判断△APB是什么三角形?证明你的结论;
2.比较DP与PC的大小;
3.如图(2)以AB为直径作半圆O,交AD于点E,连结BE与AP交于点F,若AD=5cm,AP=8cm,求证△AEF∽△APB,并求tan∠AFE的值。
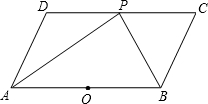 如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA.
如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA.| 4 | 3 |
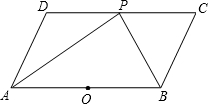 如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA.
如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA. ,求tan∠AFE的值.
,求tan∠AFE的值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com