
题目列表(包括答案和解析)
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2= ______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
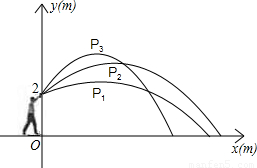
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m | ______m | 7.3m |
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2= ______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
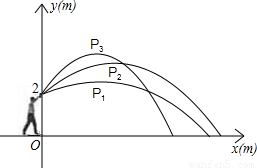
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m | ______m | 7.3m |
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2= ______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m | ______m | 7.3m |

如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如:4=22-02,12=42-22,20=62-42,因此4,12,20都是“神秘数”.
(1)28和2012这两个数是“神秘数”吗?为什么?
(2)设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么?;
(3)两个连续奇数(取正数)的平方差会是“神秘数”吗?为什么?
观察下列两组算式:(1)21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,(2)84=(23)4=23×4=212 ;由(1)(2)两组算式所揭示的规律,可知: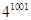 的个位数是( )
的个位数是( )
A.2 B.4 C.8 D.6
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com