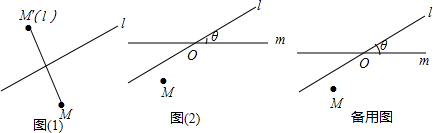
平面上的点M关于直线l有唯一的轴对称点M′,这样平面上的任意一点就与该点关于这条直线的轴对称点之间建立了一种对应关系,我们把这种对应关系叫做点M关于直线l的轴对称变换,记为
MM′(l),点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换
MM′(l),得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换
M′(l)Mn(l,m),这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为
M′(l)Mn(l,m),M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
(1)在图(2)中,求作M′(l)和M′′(l,m).(要求保留作图痕迹)
(2)当θ=
°时,M与M′′(l,m)关于点O成中心对称.
(A)30(B)45(C)60(D)90
(3)(在以下两题中任选一题作答)
①试探讨∠MOM′′(l,m)与θ之间的数量关系,并证明你的结论.
②试探讨OM与OM′′(l,m)间的数量关系,并证明你的结论.

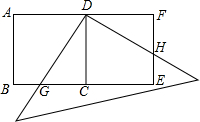
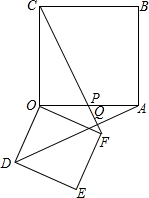
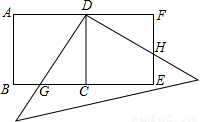
 25、友情提示:本题有A、B两题,请你任选一题作答,A题满分9分,B题满分12分.若两题都做,只能按A题评分.
25、友情提示:本题有A、B两题,请你任选一题作答,A题满分9分,B题满分12分.若两题都做,只能按A题评分.


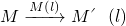 ,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换
,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换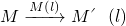 ,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换
,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换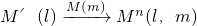 ,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为
,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为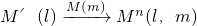 ,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题: