
题目列表(包括答案和解析)
(本小题满分12分)已知某种水果的批发单价与批发量的函数关系如图1所示.
(1)请说明图中①、②两段函数图象的实际意义.
(2)写出批发 该种水果的资金金额w(元)与
该种水果的资金金额w(元)与 批发量m(kg)之间的函数关系式;在上图的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可
批发量m(kg)之间的函数关系式;在上图的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可 以批发到较多数量的该种水果.
以批发到较多数量的该种水果.
(3)经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图(2)所示,该经销商以每日售出60kg以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大.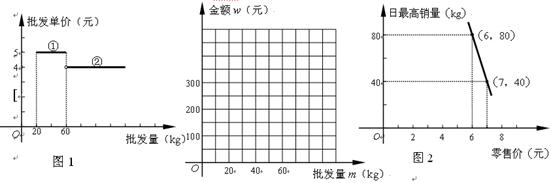
(本小题满分12分)
图中的曲线是函数![]() (m为常数)图象的一支.
(m为常数)图象的一支.
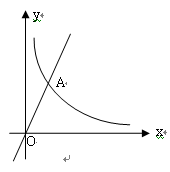
1.求常数m的取值范围;
2.若该函数的图象与正比例函数![]() 图象在第一象限的交点为A(2,n),
图象在第一象限的交点为A(2,n),
求点A的坐标及反比例函数的解析式.
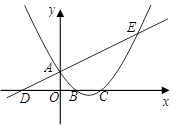
(本小题满分12分)已知:直线与
轴交于A,与
轴交于D,抛物线
与直线交于A、E两点,与
轴交于B、C两点,且B点坐标为 (1,0).
(1)求抛物线的解析式;
(2)动点P在![]() 轴上移动,当△PAE是直角三角形时,求点P的坐标.
轴上移动,当△PAE是直角三角形时,求点P的坐标.
(3)在抛物线的对称轴上找一点M,使的值最大,求出点M的坐标.
(本小题满分12分)
如图16,在直角梯形ABCD中,AD∥BC,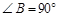 ,AD = 6,BC = 8,
,AD = 6,BC = 8,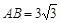 ,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.
,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.
设点P,Q运动的时间是t秒(t>0).
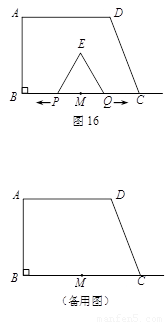
(1)设PQ的长为y,在点P从点M向点B运动的过程中,写出y与t之间的函数关系式(不必写t的取值范围).
(2)当BP = 1时,求△EPQ与梯形ABCD重叠部分的面积.
(3)随着时间t的变化,线段AD会有一部分被△EPQ覆盖,被覆盖线段的长度在某个时刻会达到最大值,请回答:该最大值能否持续一个时段?若能,直接写出t的取值范围;若不能,请说明理由.
(本小题满分12分)如下图,AB∥CD,直线a交AB、CD分别于点E、F,点M在EF上,p是直线CD上的一个动点,(点P不与F重合)
(1)当点P在射线FC上移动时,如图(1),∠FMP+∠FPM=∠AEF成立吗?请说明理由。
(2)当点P在射线FD上移动时,如图(2),∠FMP+∠FPM与∠AEF有什么关系?
说明你的理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com