练习册

  • 练习册
  • 试题
    26．已知内接于以为直径的.过点作的切线交的延长线于点.且． 【查看更多】

     

    题目列表(包括答案和解析)

    已知四边形ABCD是边长为4的正方形，以AB为直径在正方形内作半圆，P是半圆上的动点（不与点A、B重合），连接PA、PB、PC、PD．
    （1）当PA的长度为
    2
    2
    时，∠PAB=60°；
    （2）当PA的长度为
    2
    		2
    或
    8
    		5
    5
    2
    		2
    或
    8
    		5
    5
    时，△PAD是等腰三角形；
    （3）过点P作PE⊥PC交射线AB于E，延长BP交射线AD于F，试证明：AE=AF．

    查看答案和解析>>

    类比学习：
    我们已经知道，顶点在圆上，且角的两边都和圆相交的角叫做圆周角，如图1，∠APB就是圆周角，弧AB是∠APB所夹的弧．
    类似的，我们可以把顶点在圆外，且角的两边都和圆相交的角叫做圆外角，如图2，∠APB就是圆外角，弧AB和弧CD是∠APB所夹的弧，
    新知探索：
    图（2）中，弧AB和弧CD度数分别为80°和30°，∠APB=
    25
    25
    °，
    归纳总结：
    （1）圆周角的度数等于它所夹的弧的度数的一半；
    （2）圆外角的度数等于
    所夹两弧的度数差的一半
    所夹两弧的度数差的一半
    ．
    新知应用：
    直线y=-x+m与直线y=-
    		3
    3
    x+2相交于y轴上的点C，与x轴分别交于点A、B．经过A、B、C三点作⊙E，点P是第一象限内⊙E外的一动点，且点P与圆心E在直线AC的同一侧，直线PA、PC分别交⊙E于点M、N，
    设∠APC=θ．
    ①求A点坐标；         ②求⊙E的直径；
    ③连接MN，求线段MN的长度（可用含θ的三角函数式表示）．

    查看答案和解析>>

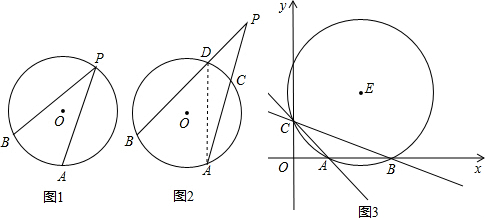
    阅读下列材料后回答问题：

    在平面直角坐标系中，已知x轴上的两点A(X1，0)，B(X2,0)的距离记作，如果是平面上任意两点，我们可以通过构造直角三角形来求A、B间的距离。

    如图，过A、B两点分别向x轴、y轴作垂线AM1、AN1和BM2、BN2，垂足分别记作，、，，直线AN1与BM2交于Q点。

    在Rt△ABQ中，，∵，

    ∴

    由此得任意两点之间的距离公式：

    如果某圆的圆心为(0,0)，半径为r。设P(x，y)是圆上任一点，根据“圆上任一点到定点(圆心)的距离都等于定长(半径)”，我们不难得到，即：，    整理得：。我们称此式为圆心在原点，半径为r的圆的方程。

    (1)直接应用平面内两点间距离公式，求点 之间的距离；

    (2)如果圆心在点P(2,3)，半径为3，求此圆的方程。

    (3)方程是否是圆的方程？如果是，求出圆心坐标与半径。

    查看答案和解析>>

    已知△ABC内接于以AB为直径的⊙O，过点C作⊙O的切线交BA的延长线于点D，且DA：AB=1：2．
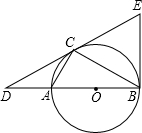    精英家教网（1）求∠CDB的度数；
    （2）在切线DC上截取CE=CD，连接EB，判断直线EB与⊙O的位置关系，并证明；
    （3）利用图中已标明的字母，连接线段，找出至少5对相似三角形（不包含全等，不需要证明）．（多写者给附加分，附加分不超过3分，计入总分，但总分不超过120分．）

    查看答案和解析>>

    已知△ABC内接于以AB为直径的⊙O，过点C作⊙O的切线交BA的延长线于点D，且DA：AB=1：2．
    （1）求∠CDB的度数；
    （2）在切线DC上截取CE=CD，连接EB，判断直线EB与⊙O的位置关系，并证明；
    （3）利用图中已标明的字母，连接线段，找出至少5对相似三角形（不包含全等，不需要证明）．

    查看答案和解析>>


    同步练习册答案