
题目列表(包括答案和解析)
 如图,△ABC是某小区的一块空地,现要加以绿化,其中点O是空地内安装喷泉的位置,它到三边的距离相等,即OD=OE=OF=m,现测得m=8.48米,三边长a=41米,b=34米,c=25米.利用因式分解求这块空地的面积.
如图,△ABC是某小区的一块空地,现要加以绿化,其中点O是空地内安装喷泉的位置,它到三边的距离相等,即OD=OE=OF=m,现测得m=8.48米,三边长a=41米,b=34米,c=25米.利用因式分解求这块空地的面积.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
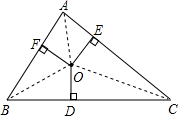 如图,△ABC是某小区的一块空地,现要加以绿化,其中点O是空地内安装喷泉的位置,它到三边的距离相等,即OD=OE=OF=m,现测得m=8.48米,三边长a=41米,b=34米,c=25米.利用因式分解求这块空地的面积.
如图,△ABC是某小区的一块空地,现要加以绿化,其中点O是空地内安装喷泉的位置,它到三边的距离相等,即OD=OE=OF=m,现测得m=8.48米,三边长a=41米,b=34米,c=25米.利用因式分解求这块空地的面积. 的一边在BC上,其余两个顶点E、F分别在AB、AC上.
的一边在BC上,其余两个顶点E、F分别在AB、AC上.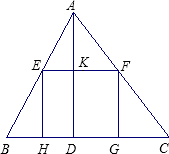 的一边在BC上,其余两个顶点E、F分别在AB、AC上.
的一边在BC上,其余两个顶点E、F分别在AB、AC上.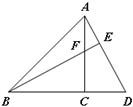 22、如图,△ABC是等腰三角形,∠ACB=90°,延长BC到D,连接AD,过点B作BE⊥AD于E,交AC于F,在这个图形中,哪两个三角形可以看成是其中一个三角形沿着某一点旋转而得到的?试说明理由.
22、如图,△ABC是等腰三角形,∠ACB=90°,延长BC到D,连接AD,过点B作BE⊥AD于E,交AC于F,在这个图形中,哪两个三角形可以看成是其中一个三角形沿着某一点旋转而得到的?试说明理由.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com