
题目列表(包括答案和解析)
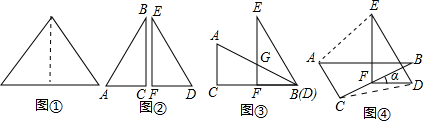

如图①所示,将一个正三角形纸片沿着它的一条边上的高剪开,得到如图②所示的两个全等的Rt△ABC、Rt△DEF.

(1)根据正三角形的性质可知:在图②中,∠ABC=∠DEF=30°,AB=DE=2AC=2DF.由此请你归纳一下在含30°角的直角三角形中,30°角所对的直角边与斜边之间的关系:
在含30°角的直角三角形中,30°角所对的直角边________;
(2)将这两个直角三角形纸片按如图③放置,使点B、D重合,点F在BC上.固定纸片DEF,将△ABC绕点F逆时针旋转角α(0°<α<90°),使四边形ACDE为以ED为底的梯形(如图④所示),求此时α的值;
(3)猜想图④中AE与CD之间的大小关系,并说明理由.

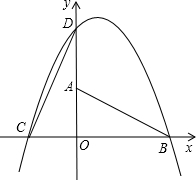 ,OB=4,现将Rt△AOB绕着直角顶点O按逆时针方向旋转90°得到△COD,已知一抛物线经过C、D、B三点.
,OB=4,现将Rt△AOB绕着直角顶点O按逆时针方向旋转90°得到△COD,已知一抛物线经过C、D、B三点.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com