有一个算式分子都是整数,满足
++≈1.16,那么你能算出他们的分子依次是哪些数吗?
在我们的教科书中选取了一些具体值并将它们代入要解的一元二次方程中,大致估计出一元二次方程解的范围,再在这个范围内逐步加细赋值,进而逐步估计出一元二次方程的近似解.下面介绍另外一种估计一元二次方程近似解的方法,以方程x
2-3x-1=0为例,因为x≠0,所以先将其变形为x=3+
,用3+
代替x,得x=3+
=3+
.反复若干次用3+
代替x,就得到x=
3+形如上式右边的式子称为连分数.
可以猜想,随着替代次数的不断增加,右式最后的
对整个式子的值的影响将越来越小,因此可以根据需要,在适当时候把
忽略不计,例如,当忽略x=3+
中的
时,就得到x=3;当忽略x=3+
中的
时,就得到x=3+
;如此等等,于是可以得到一系列分数;
3,3+
,3+
,3+
,…,即3,
=3.333…,
≈3.3.
=3.303 03…,….
可以发现它们越来越趋于稳定,事实上,这些数越来越近似于方程x
2-3x-1=0的正根,而且它的算法也很简单,就是以3为第一个近似值,然后不断地求倒数,再加3而已,在计算机技术极为发达的今天,只要编一个极为简单的程序,计算机就能很快帮你算出它的多个近似值.

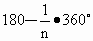 求内角的度数;
求内角的度数;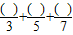 ≈1.16,那么你能算出他们的分子依次是哪些数吗?
≈1.16,那么你能算出他们的分子依次是哪些数吗?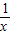 ,用3+
,用3+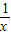 代替x,得x=3+
代替x,得x=3+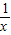 =3+
=3+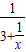 .反复若干次用3+
.反复若干次用3+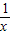 代替x,就得到x=
代替x,就得到x=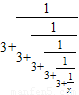 形如上式右边的式子称为连分数.
形如上式右边的式子称为连分数.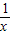 对整个式子的值的影响将越来越小,因此可以根据需要,在适当时候把
对整个式子的值的影响将越来越小,因此可以根据需要,在适当时候把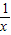 忽略不计,例如,当忽略x=3+
忽略不计,例如,当忽略x=3+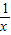 中的
中的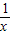 时,就得到x=3;当忽略x=3+
时,就得到x=3;当忽略x=3+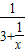 中的
中的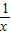 时,就得到x=3+
时,就得到x=3+ ;如此等等,于是可以得到一系列分数;
;如此等等,于是可以得到一系列分数; ,3+
,3+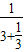 ,3+
,3+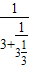 ,…,即3,
,…,即3,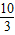 =3.333…,
=3.333…,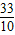 ≈3.3.
≈3.3.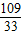 =3.303 03…,….
=3.303 03…,….