
题目列表(包括答案和解析)
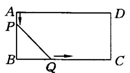
如图26-3-14所示,在矩形ABCD中,AB=6cm,BC=12cm,点P从A点出发,沿AB边向点B以1cm/s的速度移动,同时,Q点从B点出发,沿BC边向点C以2cm/s的速度移动.如果P、Q两点分别到达B、C两点后就停止移动,解答下列问题:
(1)运动开始后第几秒时,△PBQ的面积等于8cm2?
(2)设运动开始后第t秒时,五边形APQCD的面积为Scm2,写出S与t的函数关系式,并指出自变量的取值范围.

如图是2013年某月份的月历:
星期 一 二 三 四 五 六 日
1
![]() 2 3 4 5 6 7 8
2 3 4 5 6 7 8
9 10 11 12 13 14 15
16 17 18 19 20 21 22
![]() 23 24 25 26 27 28 29
23 24 25 26 27 28 29
30 31
⑴用一个平行四边形在这张月历中任意框出四个数,设左上角第一个数为x,那么右下角的数为____________,这四个数和为_______________(用x的代数式表示) .
⑵用上题的方法在这张月历中框出的四个数之和是否可能等于102?若有可能,请求出这四个数分别是几号;若不可能,试说明理由.
如图26-3-14所示,在矩形ABCD中,AB=6cm,BC=12cm,点P从A点出发,沿AB边向点B以1cm/s的速度移动,同时,Q点从B点出发,沿BC边向点C以2cm/s的速度移动.如果P、Q两点分别到达B、C两点后就停止移动,解答下列问题:
(1)运动开始后第几秒时,△PBQ的面积等于8cm2?
(2)设运动开始后第t秒时,五边形APQCD的面积为Scm2,写出S与t的函数关系式,并指出自变量的取值范围.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
 n次取走后,还剩
n次取走后,还剩| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 27 |
| 2 |
| 3n |
| 1 |
| 3n |
| 1 |
| 3n |
| 1 |
| 3 |
| 2 |
| 9 |
| 4 |
| 27 |
| 2n-1 |
| 3n |
| 2n |
| 3n |
| 2n |
| 3n |
利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.我们刚学过的《从面积到乘法公式》就很好地体现了这一思想方法,你能利用数形结合的思想解决下列问题吗?
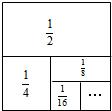
如图,一个边长为1的正方形,依次取正方形的![]() 根据图示我们可以知道:第一次取走
根据图示我们可以知道:第一次取走![]() 后还剩
后还剩![]() ,即
,即![]() =1-
=1-![]() ;前两次取走
;前两次取走![]() +
+![]() 后还剩
后还剩![]() ,即
,即![]() +
+![]() =1-
=1-![]() ;前三次取走
;前三次取走![]() +
+![]() +
+![]() 后还剩
后还剩![]() ,即
,即![]() +
+![]() +
+![]() =1-
=1-![]() ;……前n次取走后,还剩 ,
;……前n次取走后,还剩 ,
即 = .
利用上述计算:
(1) ![]() = .
= .
(2) ![]() = .
= .
(3) 2-22-23-24-25-26-…-22011+22012 (本题写出解题过程)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com