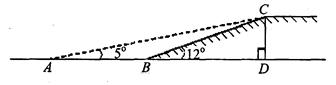
（本题满分6分）如图，有一段斜坡BC长为10米，坡角∠CBD＝12°，为方便残疾人的轮椅车通行，现准备把坡角降为5°．

【小题1】(1)求坡高CD；
【小题2】(2)求斜坡新起点A与原起点B的距离（精确到0.1米）．

（本题满分12分） 如图所示，在平面直角坐标系中，矩形ABOC的边OB在x轴的负半轴上，边OC在y轴的正半轴上，且AB=1，OB=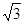，矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E，点B的对应点为F，点C的对应点为点D.  抛物线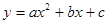过点A、E、D.

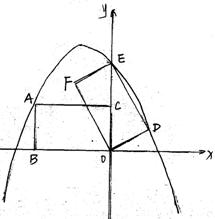
1.(1) 判断点E是否在y轴上，并说明理由；

2.（2）求抛物线的解析式；

3.（3）在x 轴的上方是否存在点P、Q，使以点O、B、P、Q为顶点的平行四边形的面积是矩形ABOC的面积的2倍，且点P在抛物线上，若存在，求P、Q两点的坐标，若不存在，请说明理由。

（本题满分9分）如图，Rt△ABC中，∠C＝90°，BC＝6，AC＝8．点P，Q都是斜边AB上的动点，点P从B向A运动（不与点B重合），点Q从A向B运动，BP＝AQ．点D，E分别是点A，B以Q，P为对称中心的对称点，HQ⊥AB于Q，交AC于点H．当点E到达顶点A时，P、Q同时停止运动．设BP的长为x，△HDE的面积为y．

1.(1)求证：△DHQ∽△ABC；

2.(2)求y关于x的函数解析式并求y的最大值；

3.(3)当x为何值时，△HDE为等腰三角形？