题目列表(包括答案和解析)
先阅读，再填空解题：
(1)方程
的根是
，
，则
，
；
(2)方程
的根是
，
，则
，
。
(3)方程
的根是
，
，则
， 
。
根据以上(1) (2) (3)你能否猜出：
如果关于
的一元二次方程
(m≠0，且m、n、p为常数)的两个实数根是
、
，那么
，
与系数m、n、p有什么关系?请写出你的猜想。(不说明理由)
阅读材料：
如果x1，x2是一元二次方程ax2+bx+c=0的两根，那么有：x1+x2= -
，x1x2=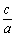
。这是一元二次方程根与系数的关系，我们利用它可以用来解题
例：x1，x2是方程x2+6x-3=0的两根，求x12+x22的值。
解法可以这样：x1+x2=-6，x1x2= -3，则 x12+x22=(x1+x2)2-2x1x2=(-6)2-2(-3)= 42。
请你根据以上解法解答下题：
已知x1，x2是方程x2-4x+2=0的两根，求：
（1）
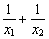的值；
（2）（x1-x2）2的值。
，
，
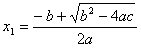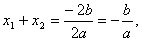
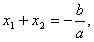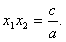
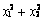的值。解法可以这样：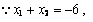
则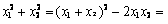
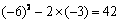。小明是一位刻苦学习、勤于思考、勇于创新的同学。一天，他在解方程时，突然产生了这样的想法：
这个方程在实数范围内无解，如果存在一个数
使
，那么方程可以变为
，则
，从而是方程的两个根．小明还发现具有如下性质：
……
请你观察上述等式，根据发现的规律填空：
，
，
，
（
为自然数）
这个方程在实数范围内无解，如果存在一个数
使
，那么方程可以变为
，则
，从而是方程的两个根．小明还发现具有如下性质：
……
，
，
，
（
为自然数）湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com