
题目列表(包括答案和解析)

| 5 | 2 |

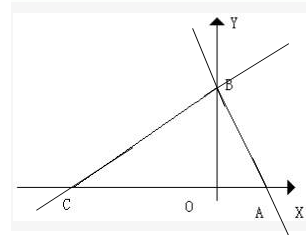
如图,在平面直角坐标系中,点C(-3,0),点A、B分别在x轴,y轴的正半轴上,且满足![]() .
.
1.求点A、B坐标
2.若点P从点C出发,以每秒1个单位的速度沿射线CB运动,连接AP。设△ABP面积为S,点P的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围
3.在(2)的条件下,是否存在点P,使以点A、B、P为顶点的三角形与△AOB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由。(本题满分8分)
计算(本题满分12分,每题4分)
(1) ―12012+ (![]() )-1―(3.14-π)0
)-1―(3.14-π)0
(2) (-6xy2)2(―![]() xy +
xy + ![]() y2―x2)
y2―x2)
(3) 先化简,再求值:(2m+n)2-(3m-n)2+5m(m-n),其中m=![]() ,n=
,n=![]() .
.
解不等式组 ,并把它的解集在数轴上表示出来。(本题满分5分)
,并把它的解集在数轴上表示出来。(本题满分5分)
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
B
C
B
D
A
D
D
C
二、填空题
题 号
11
12
13
14
15
答 案
2<x<8
(-3,-7)

34.28
三、解答题(本大题有7题,共55分)
16.1
17.经检验:x1=0,x2=2是原方程的根.
18.解:(1)根据题意有AF∥BC,∴∠ACB=∠GAF,又 ∠ABC=∠AFG=90 ,
,
∴△ABC∽△GFA
∴
 ,得BC=3.2(m),CD=(2+3)-3.2=1.8(m)
,得BC=3.2(m),CD=(2+3)-3.2=1.8(m)
(2)设楼梯应建x个台阶,则,
解得,14<x<16
∴楼梯应建15个台阶
19.(1) (2)
(2)



 不公平改为“如果和为0,李明得3分,其余不变
不公平改为“如果和为0,李明得3分,其余不变
20.解:(1)△AEF是等边三角形.
由折叠过程易得:
∵BC∥AD,∴
∴△AEF是等边三角形.
(2)不一定.
当矩形的长恰好等于等边△AEF的边AF时,
即矩形的宽∶长=AB∶AF=sin60°= 时正好能折出.
时正好能折出.
如果设矩形的长为a,宽为b,
可知当 时,按此法一定能折出等边三角形;
时,按此法一定能折出等边三角形;
当 时,按此法无法折出完整的等边三角形.
时,按此法无法折出完整的等边三角形.
21.(1)证明:∵AB = AC,点D是边BC的中点,∴AD⊥BD.
又∵BD是圆O直径,∴AD是圆O的切线.
(2)解:连结OP,OE.
由BC = 8,得CD = 4,OC = 6,OP = 2.
∵PC是圆O的切线,O为圆心,∴ .
.
于是,利用勾股定理,得 .
.
∵ ,
, ,
,
∴△DCE∽△PCO.
∴ ,即得
,即得 .
.
∵PE、DE是圆O的切线,∴ .
.
于是,由 ,得
,得 .
.
又∵OB = OP,∴ .
.
于是,由 ,得
,得 .
.
∴ .∴OE // AB.
.∴OE // AB.
∴ ,即得
,即得 .
.
∴ .
.
22. 解:(1)因为二次函数y=ax2+bx+c的图象经过点A(-1,0)、B(3,0)、N(2,3)
所以,可建立方程组: ,解得:
,解得:
所以,所求二次函数的解析式为y=-x2+2x+3,
所以,顶点M(1,4),点C(0,3) -------2分
(2)直线y=kx+d经过C、M两点,所以 ,即k=1,d=3,
,即k=1,d=3,
直线解析式为y=x+3
令y=0,得x=-3,故D(-3,0)
∴ CD= ,AN=
,AN= ,AD=2,CN=2
,AD=2,CN=2
∴CD=AN,AD=CN
∴ 四边形CDAN是平行四边形
(3)假设存在这样的点P,使以点P为圆心的圆经过A、B两点,并且与直线CD相切,因为这个二次函数的对称轴是直线x=1,故可设P(1, ),
),
则PA是圆的半径且PA2=y02+22,
过P作直线CD的垂线,垂足为Q,则PQ=PA时以P为圆心的圆与直线CD相切。
由第(2)小题易得:△MDE为等腰直角三角形,故△PQM也是等腰直角三角形,
由P(1, )得PE=
)得PE= ,PM=|4-
,PM=|4- |,
|, ,
,
由PQ2=PA2得方程: ,解得
,解得 ,符合题意,
,符合题意,
所以,满足题意的点P存在,其坐标为(1, )或(1,
)或(1, )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com