
题目列表(包括答案和解析)
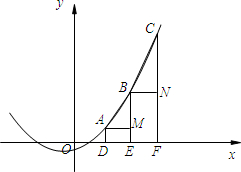 在函数中,我们规定:当自变量增加一个单位时,因变量的增加量称为函数的平均变化率.例如,对于函数y=3x+1,当自变量x增加1时,因变量y=3(x+1)+1=3x+4,较之前增加3,故函数y=3x+1的平均变化率为3.
在函数中,我们规定:当自变量增加一个单位时,因变量的增加量称为函数的平均变化率.例如,对于函数y=3x+1,当自变量x增加1时,因变量y=3(x+1)+1=3x+4,较之前增加3,故函数y=3x+1的平均变化率为3.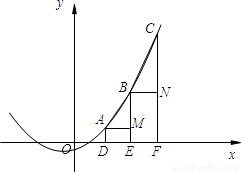
 .水槽中水面上升的高度h与注水时间t之间的函数关系如图所示.
.水槽中水面上升的高度h与注水时间t之间的函数关系如图所示. 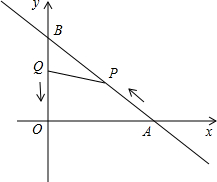 段BO上,以1个单位/秒的速度向点O移动,设移动的时间为t(秒)
段BO上,以1个单位/秒的速度向点O移动,设移动的时间为t(秒) 段BO上,以1个单位/秒的速度向点O移动,设移动的时间为t(秒)
段BO上,以1个单位/秒的速度向点O移动,设移动的时间为t(秒)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com