
题目列表(包括答案和解析)
|
| y |
| x-1 |
设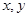 满足约束条件:
满足约束条件: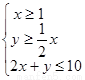 的可行域为
的可行域为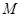
1)在所给的坐标系中画出可行域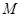 (用阴影表示,并注明边界的交点或直线);
(用阴影表示,并注明边界的交点或直线);
2)求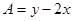 的最大值与
的最大值与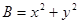 的最小值;
的最小值;
3)若存在正实数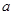 ,使函数
,使函数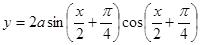 的图象经过区域
的图象经过区域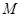 中的点,
中的点,
求这时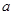 的取值范围.
的取值范围.
某农场预算用5600元购买单价为50元(每吨)的钾肥和20元(每吨)的氮肥,希望使两种肥料的总数量(吨)尽可能的多,但氮肥吨数不少于钾肥吨数,且不多于钾肥吨数的1.5倍.
(1) 设买钾肥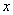 吨,买氮肥
吨,买氮肥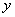 吨,按题意列出约束条件、画出可行域,并求钾肥、氮肥各买多少才行?
吨,按题意列出约束条件、画出可行域,并求钾肥、氮肥各买多少才行?
(2) 设点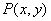 在(1)中的可行域内,求
在(1)中的可行域内,求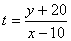 的取值范围;
的取值范围;
(3) 已知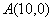 ,O是原点,
,O是原点, 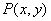 在(1)中的可行域内,求
在(1)中的可行域内,求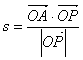 的取值范围.
的取值范围.
如图,直线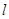 与抛物线
与抛物线 交于
交于 两点,与
两点,与 轴相交于点
轴相交于点 ,且
,且 .
.
(1)求证: 点的坐标为
点的坐标为 ;
;
(2)求证: ;
;
(3)求 的面积的最小值.
的面积的最小值.

【解析】设出点M的坐标 ,并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论,可以设其方程为
,并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论,可以设其方程为 ,然后与抛物线方程联立消x,根据
,然后与抛物线方程联立消x,根据 ,即可建立关于
,即可建立关于 的方程.求出
的方程.求出 的值.
的值.
(2)在第(1)问的基础上,证明: 即可.
即可.
(3)先建立面积S关于m的函数关系式,根据 建立即可,然后再考虑利用函数求最值的方法求最值.
建立即可,然后再考虑利用函数求最值的方法求最值.
已知曲线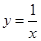 和
和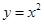 相交于点A,
相交于点A,
(1)求A点坐标;
(2)分别求它们在A点处的切线方程(写成直线的一般式方程);
(3)求由曲线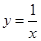 在A点处的切线及
在A点处的切线及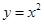 以及
以及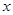 轴所围成的图形面积。(画出草图)
轴所围成的图形面积。(画出草图)
【解析】本试题主要考察了导数的几何意义的运用,以及利用定积分求解曲边梯形的面积的综合试题。先确定切点,然后求解斜率,最后得到切线方程。而求解面积,要先求解交点,确定上限和下限,然后借助于微积分基本定理得到。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com