我们知道：有两条边相等的三角形叫做等腰三角形。类似地，我们定义：至少有一级对边相等的四边形叫做等对边四边形。

(1)请写出一个你学过的特殊四边形中是等对边四边形的图形的名称；

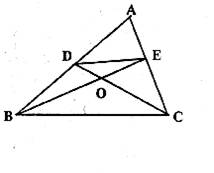
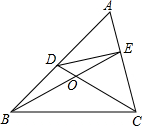
(2)如图，在A ABC中，点D、E分别在AB、AC上，设CD、BE相交于点O,若∠A=60°，∠DCB=∠EBC=∠A，请写出图中一个与∠A相等的角．并猜想图中哪个四边形是等对边四形；

(3)在△ABC中，如果∠A是不等于60°的锐角，占D、E分别在AB、AC上，且∠DCB=∠EBC=∠A，探究：满足上述条件的图形中是否存在等对边四边形，并证明你的结论。

已知△ABC，分别以AB、AC为边作△ABD和△ACE，且AD=AB，AC=AE，∠DAB=∠CAE，连接DC与BE，G、F分别是DC与BE的中点．
（1）如图1，若∠DAB=60°，则∠AFG=______；如图2，若∠DAB=90°，则∠AFG=______；
（2）如图3，若∠DAB=α，试探究∠AFG与α的数量关系，并给予证明；
（3）如果∠ACB为锐角，AB≠AC，∠BAC≠90°，点M在线段BC上运动，连接AM，以AM为一边以点A为直角顶点，且在AM的右侧作等腰直角△AMN，连接NC；试探究：若NC⊥BC（点C、M重合除外），则∠ACB等于多少度？画出相应图形，并说明理由．（画图不写作法）

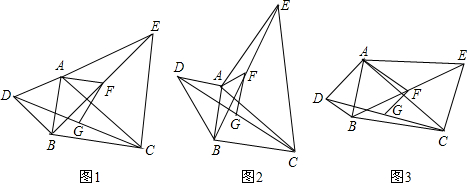
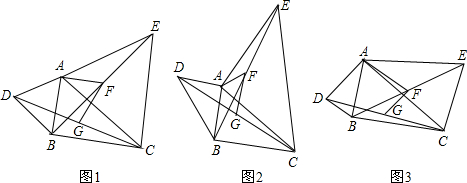
已知△ABC，分别以AB、AC为边作△ABD和△ACE，且AD=AB，AC=AE，∠DAB=∠CAE，连接DC与BE，G、F分别是DC与BE的中点．

（1）如图1，若∠DAB =60°，则∠AFG=__     ____；

如图2，若∠DAB =90°，则∠AFG=____     __；

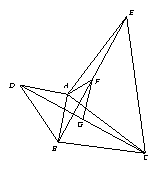
图1                                    图2

（2）如图3，若∠DAB =，试探究∠AFG与的数量关系，并给予证明．；

（3）如果∠ACB为锐角，AB≠AC，∠BAC≠90º，点M在线段BC上运动，连接AM，以AM为一边以点A为直角顶点，且在AM的右侧作等腰直角△AMN，连接NC；

试探究：若NC⊥BC（点C、M重合除外），则∠ACB等于多少度？画出相应图形，并说明理由．（画图不写作法）