题目列表(包括答案和解析)
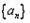的前n项和为Sn，满足
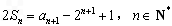，且
、
、
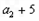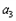成等差数列。
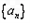的通项公式；
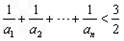。设数列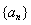
的前n项和为
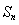，已知
，
，
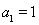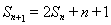
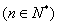（1）求数列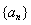的通项公式；
（2）若
，数列
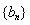的前n项和为
，
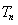，证明：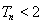
.
设数列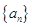
的前n项和为
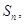已知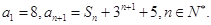
（Ⅰ）设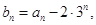
证明：数列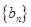
是等比数列；
（Ⅱ）证明：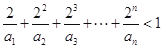
.
设数列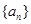
的前n项和为
，
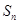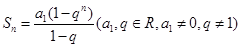
（1）求证：数列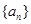是等比数列；
（2）若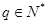
，是否存在q的某些取值，使数列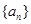中某一项能表示为另外三项之和？若能求出q的全部取值集合，若不能说明理由。
（3）若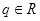
，是否存在
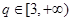，使数列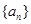中，某一项可以表示为另外三项之和？若存在指出q的一个取值，若不存在，说明理由。
设数列
的前n项和为
，已知
，
，
（1）求数列的通项公式；
（2）若
，数列
的前n项和为
，
，证明：
.
一、选择题: B A B D A B D C B D Ｂ Ｃ
二、填空题： 13.
14．－８
15．1 16．①②
三、解答题：
18．解：依题意，第四项指标抽检合格的概率为 
其它三项指标抽检合格的概率均为
。
（1）若食品监管部门对其四项质量指标依次进行严格的检测，恰好在第三项指标检测结束时， 能确定该食品不能上市的概率等于第一、第二项指标中恰有一项不合格而且第三项指标不合格的概率．
(2)该品牌的食品能上市的概率等于四项指标都含格或第一、第二、第三项指标中仅有
一项不合格且第四项指标合格的概率．
故二面角
的大小为
解法二：如图，以
为原点，建立空间直角坐标系，使
轴，
、
分别在
轴、
轴上。
（1）由已知，
，
，
，
，
，
，
∴
， 
，
，
∵
， ∴
，
又
，∴
21.解：（1）设直线
的方程为
，联立，得
由△
得,
或
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com