
题目列表(包括答案和解析)
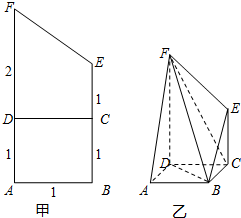 将(如图甲)直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连接部分线段后围成一个空间几何体,如图乙所示.
将(如图甲)直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连接部分线段后围成一个空间几何体,如图乙所示.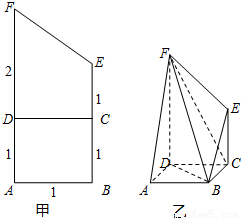
(1)现从中取出四个,可能出现的不同结果有几种?
(2)若取出四个后排成一排,又有几种不同的排法?
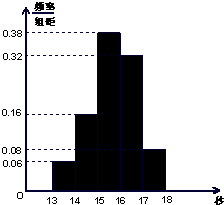 (2012•珠海二模)某学校900名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
(2012•珠海二模)某学校900名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.| 6 |
1.A 2.D 3.C 4.B 5.B 6.A 7.B 8.C 9.A 10.C 11.C 12.D
13.(1-a) 14.2 15. 16.
17.解:(1)∵p,q共线,
∴(2-2sin A)(1+sin A)=(cos A+sin A)(sin A-cos A),1分
∴sin2A=.2分
∵cos Acos Bcos C>0,∴A为锐角.3分
∴sin A=,∴A=.5分
(2)y=2sin2B+cos=2sin2B+cos6分
=2sin2B+cos(-2B)=1-cos 2B+cos 2B+sin 2B8分
=sin 2B-cos 2B+1=sin(2B-)+1.10分
∵B∈(0,),∴2B-∈(-,).11分
∴当2B-=时,即B=时,ymax=2.12分
18.解:(1)由题意可知ξ甲~B(5,p1),
∴Dξ甲=5p1(1-p1)=1分
⇒p-p1+=03分
⇒p1=.4分
又?=6,∴p2=.6分
(2)分两类情况:①共击中3次概率C()2()6?C()()+C??C()2=.9分
②共击中4次概率C()2?C()2=.11分
所求概率为+=.12分
19.解:(1)由函数f(x)=-x4+x3+ax2-2x-2在区间[-1,1]上是单调递减,在区间[1,2]上单调递增,所以x=1取得极小值.1分
∴f′(1)=0,∴-1+2+2a-2=0,3分
∴a=.4分
(2)由(1)知f(x)=-x4+x3+x2-2x-2,
∴f′(x)=-x3+2x2+x-2.5分
令f′(x)=0,得x=-1,x=1,x=2.6分
∴函数f(x)有极大值f(-1)=-,f(2)=-,极小值f(1)=-.8分
关于x的方程f(2|x|-1)=m(x≠0)有六个不同的实数解,令2|x|-1=t(t>0),
即关于t的方程f(t)=m在t∈(0,+∞)上有三个不同的实数解.9分
在t∈(0,+∞)上函数f(t)的图象与直线y=m的图象在t∈(0,+∞)上有三个不同的交点,而f(t)的图象与f(x)的图象一致.11分
又f(0)=-2,由数形结合可知,-<m<-.12分
20.解:(1)延长CG交AB于N,∵G是△ABC的重心,∴N是AB的中点.1分
∵∠ACB=90°,∴CN=AB=6,∴CG=CN=4.2分
作ME∥GC交DC于E,∴∠EMB是异面直线GC与BM所成的角或补角.3分
∵M是DG的中点,ME=GC=2,
BE===2.4分
过M作MH⊥GC于H,MH⊥平面ABC,∴MH=2,
∴MB2=MH2+HB2=4+4+36-2?2?6?cos 60°=32,
∴cos∠EMB==-.5分
∴异面直线GC与BM所成的角为arccos.6分
(2)++=-(++),
∵G是△ABC的重心,
∴++=3.7分
∴(++)?=-3?.8分
△DGC是等腰直角三角形,DG=CD=4.9分
设MG=x,则MD=4-x,
∴-3?=-3||||cos 180°=3?x?(4-x)10分
≤3()2=24.11分
∴(++)?的最大值是24.
(当且仅当M为GD的中点时取得).12分
(备注:以上各小题都可以通过建立空间直角坐标系求解,建议参照给分)
21.解:(1)由|PF1|-|PF2|=2<|F1F2|知,
点P的轨迹S是以F1、F2为焦点的双曲线右支.1分
由c=2,2a=2,∴b2=3.2分
故轨迹S的方程为x2-=1(x≥1).4分
(2)当直线l的斜率存在时,设直线方程为y=k(x-2),P(x1,y1),Q(x2,y2)与双曲线方程联立消y得(k2-3)x2-4k2x+4k2+3=0.
∴解得k2>3.5分
∵?=(x1-m)(x2-m)+y1y2
=(x1-m)(x2-m)+k2(x1-2)(x2-2)
=(k2+1)x1x2-(2k2+m)(x1+x2)+m2+4k2
=+m2.6分
∵MP⊥MQ,∴?=0,
故得3(1-m2)+k2(m2-4m-5)=0对任意的k2>3恒成立,
∴解得m=-1.7分
当m=-1时,MP⊥MQ,
当直线l的斜率不存在时,由P(2,3),Q(2,-3)及M(-1,0)知结论也成立.
综上,当m=-1时,MP⊥MQ.8分
(3)由(1)知,存在M(-1,0)使得MP⊥MQ,
∴∠AEP=∠MEF=∠BQF,∴△PAE~△FBE,
∴=.9分
|AE|?|FB|=|AP|?|BQ|=?=|PF2|?|OF2|,
|PF2|=ex1-a=2x1-1,|PF2|=ex2-a=2x2-1,
∴|AE||FB|=(2x1-1)(2x2-1)10分
=[4x1x2-2(x1+x2)+1]=x1x2-+
=-+=+=+>.
当斜率不存在时|AE|?|AF|=,∴λ的最小值为.11分
此时,|PQ|=6,|MF|=3,S△PMQ=|MQ|?|PQ|=9.12分
22.解:(1)由An=(an-1),An+1=(an+1-1),1分
∴an+1=(an+1-an),即=3,2分
且a1=A1=(a1-1),
得a1=3.3分
∴数列{an}是以3为首项,3为公比的等比数列.4分
通项公式为an=3n.5分
(2)∵2nln an=2nln 3n=(nln 3)?2n
=2nln 3?2n-1=2nln 3(1+1)n-16分
=2nln 3(C+C+…+C)7分
=2nln 3(nC+nC+nC+…+nC)8分
=2nln 3(C+2C+…+kC+…nC)9分
=(2ln 3)C+(2ln 3)?2C+…+(2ln 3)?kC+…+(2ln 3)?nC.12分
故存在等差数列{cn},cn=(2ln 3)?n对一切正整数n∈N*,c1C+c2C+…+cnC=2nln an都成立.14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com