
题目列表(包括答案和解析)






 的方程;
的方程; 为椭圆上任意一点,以
为椭圆上任意一点,以 为圆心,
为圆心, 为半径作圆
为半径作圆 ,当圆
,当圆 与椭圆的右准线
与椭圆的右准线 有公共点时,求△
有公共点时,求△ 面积的最大值
面积的最大值椭圆 的方程为
的方程为 ,离心率为
,离心率为 ,且短轴一端点和两焦点构成的三角形面积为1,抛物线
,且短轴一端点和两焦点构成的三角形面积为1,抛物线 的方程为
的方程为 ,抛物线的焦点F与椭圆的一个顶点重合.
,抛物线的焦点F与椭圆的一个顶点重合.
(1)求椭圆 和抛物线
和抛物线 的方程;
的方程;
(2)过点F的直线交抛物线 于不同两点A,B,交y轴于点N,已知
于不同两点A,B,交y轴于点N,已知 的值.
的值.
(3)直线 交椭圆
交椭圆 于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足
于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足 (O为原点),若点S满足
(O为原点),若点S满足 ,判定点S是否在椭圆
,判定点S是否在椭圆 上,并说明理由.
上,并说明理由.
 的方程为
的方程为 ,离心率为
,离心率为 ,且短轴一端点和两焦点构成的三角形面积为1,抛物线
,且短轴一端点和两焦点构成的三角形面积为1,抛物线 的方程为
的方程为 ,抛物线的焦点F与椭圆的一个顶点重合.
,抛物线的焦点F与椭圆的一个顶点重合. 和抛物线
和抛物线 的方程;
的方程; 于不同两点A,B,交y轴于点N,已知
于不同两点A,B,交y轴于点N,已知 的值.
的值. 交椭圆
交椭圆 于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足
于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足 (O为原点),若点S满足
(O为原点),若点S满足 ,判定点S是否在椭圆
,判定点S是否在椭圆 上,并说明理由.
上,并说明理由.设椭圆的方程为 ,斜率为1的直线不经过原点
,斜率为1的直线不经过原点 ,而且与椭圆相交于
,而且与椭圆相交于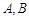 两点,
两点, 为线段
为线段 的中点.
的中点.
(1)问:直线 与
与 能否垂直?若能,求
能否垂直?若能,求 之间满足的关系式;若不能,说明理由;
之间满足的关系式;若不能,说明理由;
(2)已知 为
为 的中点,且
的中点,且 点在椭圆上.若
点在椭圆上.若 ,求
,求 之间满足的关系式.
之间满足的关系式.
设椭圆的方程为 ,斜率为1的直线不经过原点
,斜率为1的直线不经过原点 ,而且与椭圆相交于
,而且与椭圆相交于 两点,
两点, 为线段
为线段 的中点.
的中点.
(1)问:直线 与
与 能否垂直?若能,
能否垂直?若能, 之间满足什么关系;若不能,说明理由;
之间满足什么关系;若不能,说明理由;
(2)已知 为
为 的中点,且
的中点,且 点在椭圆上.若
点在椭圆上.若 ,求椭圆的离心率.
,求椭圆的离心率.
一、选择题:BDCCB BADCA
二、填空题: 11. 2
12. 试题卷与评分标准.files/image160.gif)
13. 试题卷与评分标准.files/image162.gif) 14.
14. 试题卷与评分标准.files/image164.gif)
三、解答题:
15、解:依题意得:(1)试题卷与评分标准.files/image166.gif) =0,解之得m=0或m=3
=0,解之得m=0或m=3
∴当m=0或m=3时,复数试题卷与评分标准.files/image109.gif) 是实数; ……………4分
是实数; ……………4分
(2)试题卷与评分标准.files/image166.gif) ≠0,解之得m≠0且m≠3
≠0,解之得m≠0且m≠3
∴当m≠0且m≠3时,复数试题卷与评分标准.files/image109.gif) 是虚数;……………8分
是虚数;……………8分
(3)试题卷与评分标准.files/image169.gif) ,解之得m=3
,解之得m=3
∴当m=3时,复数试题卷与评分标准.files/image109.gif) 是纯虚数. ……………12分
是纯虚数. ……………12分
16、解:(1)∵试题卷与评分标准.files/image170.gif) ∴
∴试题卷与评分标准.files/image172.gif) 两边平方相加,
两边平方相加,
得试题卷与评分标准.files/image174.gif) 即
即 试题卷与评分标准.files/image176.gif) . ………………4分
. ………………4分
∴曲线是长轴在x轴上且为10,短轴为8,中心在原点的椭圆. ………6分
(2)∵试题卷与评分标准.files/image177.gif) ∴由
∴由试题卷与评分标准.files/image179.gif) 代入
代入试题卷与评分标准.files/image181.gif) ,
,
得 试题卷与评分标准.files/image183.gif) ∴
∴试题卷与评分标准.files/image185.gif) ……………10分
……………10分
∴它表示过(0,试题卷与评分标准.files/image187.gif) )和(1, 0)的一条直线.
…………12分
)和(1, 0)的一条直线.
…………12分
17、解:(Ⅰ)试题卷与评分标准.files/image189.gif) ,
………1分
,
………1分
试题卷与评分标准.files/image191.gif) . ………2分
. ………2分
试题卷与评分标准.files/image193.gif) ,
,试题卷与评分标准.files/image195.gif) . ………4分
. ………4分
椭圆的方程为试题卷与评分标准.files/image197.gif) ,
………5分
,
………5分
因为试题卷与评分标准.files/image199.gif) ………6分
………6分
所以离心率试题卷与评分标准.files/image201.gif) . ………8分
. ………8分
(Ⅱ)设试题卷与评分标准.files/image203.gif) 的中点为
的中点为试题卷与评分标准.files/image205.gif) ,则点
,则点试题卷与评分标准.files/image207.gif) . ………10分
. ………10分
又点K在椭圆上,则试题卷与评分标准.files/image203.gif) 中点的轨迹方程为
中点的轨迹方程为试题卷与评分标准.files/image209.gif) ………14分
………14分
18、解:(1)列出2×2列联表
说谎
不说谎
合计
女生
15
5
20
男生
10
20
30
合计
25
25
50
…………6分
(2)假设H0 "说谎与性别无关",则随机变量K2的观测值:
试题卷与评分标准.files/image211.gif) ……………10分
……………10分
∴试题卷与评分标准.files/image213.gif) ,而
,而试题卷与评分标准.files/image215.gif) ……………………12分
……………………12分
所以有99.5%的把握认为"说谎与性别有关". ……………14分
19、解:(1)
试题卷与评分标准.files/image217.gif)
………………4分
(2)试题卷与评分标准.files/image219.gif) ,0×5+1×7+2×8+3×11+4×19=132,
,0×5+1×7+2×8+3×11+4×19=132,试题卷与评分标准.files/image136.gif)
试题卷与评分标准.files/image221.gif) …………8分
…………8分
故Y关于x的线性回归方程为 y=3.2x+3.6 ………10分
(3)x=5,y=196(万)
据此估计2005年.该 城市人口总数196(万) ………14分
20、解:(1)设椭圆的半焦距为试题卷与评分标准.files/image223.gif) ,依题意
,依题意 试题卷与评分标准.files/image225.gif) ………2分
………2分
∴ 试题卷与评分标准.files/image227.gif) ,∴ 所求椭圆方程为
,∴ 所求椭圆方程为试题卷与评分标准.files/image229.gif) .
………4分
.
………4分
(2)设试题卷与评分标准.files/image231.gif) ,
,试题卷与评分标准.files/image233.gif) .
.
当试题卷与评分标准.files/image235.gif) 轴时,
轴时,试题卷与评分标准.files/image237.gif) .
………5分
.
………5分
当试题卷与评分标准.files/image239.gif) 与
与试题卷与评分标准.files/image241.gif) 轴不垂直时,设直线
轴不垂直时,设直线试题卷与评分标准.files/image239.gif) 的方程为
的方程为试题卷与评分标准.files/image244.gif) . ………6分
. ………6分
由已知试题卷与评分标准.files/image246.gif) ,得
,得试题卷与评分标准.files/image248.gif) .
………7分
.
………7分
把试题卷与评分标准.files/image244.gif) 代入椭圆方程,整理得
代入椭圆方程,整理得试题卷与评分标准.files/image251.gif) ,………8分
,………8分
试题卷与评分标准.files/image253.gif) ,
,试题卷与评分标准.files/image255.gif) .………10分
.………10分
试题卷与评分标准.files/image257.gif)
试题卷与评分标准.files/image259.gif)
试题卷与评分标准.files/image261.gif)
试题卷与评分标准.files/image263.gif) . ………12分
. ………12分
当且仅当试题卷与评分标准.files/image265.gif) ,即
,即试题卷与评分标准.files/image267.gif) 时等号成立.当
时等号成立.当试题卷与评分标准.files/image269.gif) 时,
时,试题卷与评分标准.files/image237.gif) ,
,
综上所述试题卷与评分标准.files/image272.gif) .
………13分
.
………13分
试题卷与评分标准.files/image274.gif) 当
当试题卷与评分标准.files/image276.gif) 最大时,
最大时,试题卷与评分标准.files/image278.gif) 面积取最大值
面积取最大值试题卷与评分标准.files/image280.gif) .………14分
.………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com