
题目列表(包括答案和解析)

| 5 | 2 |

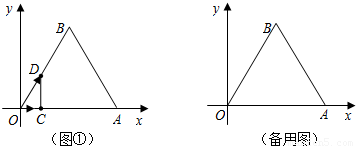
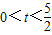 时,证明DC⊥OA;
时,证明DC⊥OA;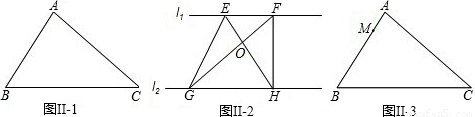
(2010 江苏镇江)推理证明(本小题满分7分)
如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,连结OE,CD=![]() ,∠ACB=30°.
,∠ACB=30°.
(1)求证:DE是⊙O的切线;
(2)分别求AB,OE的长;
(3)填空:如果以点E为圆心,r为半径的圆上总存在不同的两点到点O的距离为1,则r的取值范围为 .

一节数学课后,老师布置了一道课后练习:
如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC于点O,点P,D分别在AO和BC上,PB=PD,DE⊥AC于点E。
求证:△BPO≌△PDE。
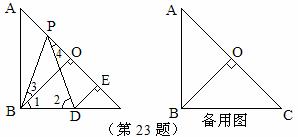
(1)理清思路,完成解答
本题证明的思路可以用下列框图表示:
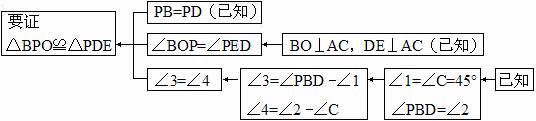
根据上述思路,请你完整地书写本题的证明过程。
(2)特殊位置,证明结论
若BP平分∠ABO,其余条件不变,求证:AP=CD;
(3)知识迁移,探索新知
若点P是一个动点,当点P运动到OC的中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系(不必写解答过程)。
一节数学课后,老师布置了一道课后练习题:
如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC,于点O,点PD分别在AO和BC上,PB=PD,DE⊥AC于点E,求证:△BPO≌△PDE.
(1)理清思路,完成解答(2)本题证明的思路可用下列框图表示:
根据上述思路,请你完整地书写本题的证明过程.
(2)特殊位置,证明结论
若PB平分∠ABO,其余条件不变.求证:AP=CD.
(3)知识迁移,探索新知
若点P是一个动点,点P运动到OC的中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系.(不必写解答过程)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com