在图1-3中，正方形ABCD的边长为a，等腰直角三角形FAE的斜边AE=2b，且边AD和AE在同一直线上．

（1）操作发现：
①当2b＜a时，如图1，在BA上选取点G，使BG=b，连接FG和CG，裁掉△FAG和△CGB，小明发现：如果先将△FAG绕点F逆时针旋转90°到△FEH的位置，那么△CGB恰可以拼接到△CHD的位置．请说明理由；
②对于拼接成的新四边形FGCH，小明通过度量发现其恰是正方形．请说明理由．
（2）实践探究：
小明进一步探究后发现：当2b＜a、2b=a、a＜2b＜2a、b=a时（即b≤a时），此类图形都能剪拼成正方形，且所选取的点G的位置在BA方向上随着b的增大不断上移．请你类比图1的剪拼方法，在图2（a＜2b＜2a）中画出剪拼成一个新正方形的示意图．
（3）联想拓展：
当b＞a时，如图3的图形能否剪拼成一个正方形？若能，请你在图中画出剪拼的示意图；若不能，简要说明理由．

在图1-3中，正方形ABCD的边长为a，等腰直角三角形FAE的斜边AE=2b，且边AD和AE在同一直线上．

（1）操作发现：
①当2b＜a时，如图1，在BA上选取点G，使BG=b，连接FG和CG，裁掉△FAG和△CGB，小明发现：如果先将△FAG绕点F逆时针旋转90°到△FEH的位置，那么△CGB恰可以拼接到△CHD的位置．请说明理由；
②对于拼接成的新四边形FGCH，小明通过度量发现其恰是正方形．请说明理由．
（2）实践探究：
小明进一步探究后发现：当2b＜a、2b=a、a＜2b＜2a、b=a时（即b≤a时），此类图形都能剪拼成正方形，且所选取的点G的位置在BA方向上随着b的增大不断上移．请你类比图1的剪拼方法，在图2（a＜2b＜2a）中画出剪拼成一个新正方形的示意图．
（3）联想拓展：
当b＞a时，如图3的图形能否剪拼成一个正方形？若能，请你在图中画出剪拼的示意图；若不能，简要说明理由．

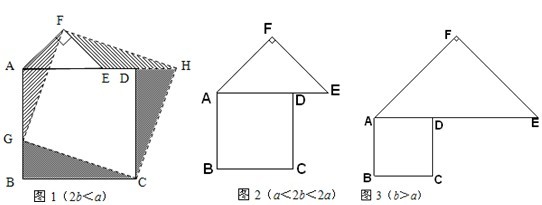
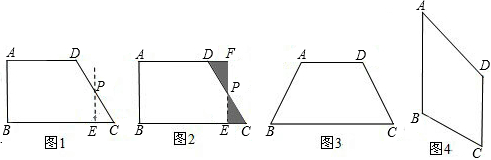
如图1，在直角梯形ABCD中，AD∥BC，∠B=∠A=90°，AD=a，BC=b，AB=c，
操作示例：
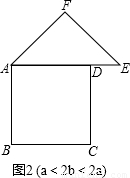
我们可以取直角梯形ABCD的非直角腰CD的中点P，过点P作PE∥AB，裁掉△PEC，并将△PEC拼接到△PFD的位置，构成新的图形（如图2）．
思考发现：
小明在操作后发现，该剪拼方法就是先将△PEC绕点P逆时针旋转180°到△PFD的位置，易知PE与PF在同一条直线上．又因为在梯形ABCD中，AD∥BC，∠C+∠ADP=180°，则∠FDP+∠ADP=180°，所以AD和DF在同一条直线上，那么构成的新图形是一个四边形，进而根据平行四边形的判定方法，可以判断出四边形ABEF是一个平行四边形，而且还是一个特殊的平行四边形--矩形．
实践探究：
（1）矩形ABEF的面积是；（用含a，b，c的式子表示）
（2）类比图2的剪拼方法，请你就图3和图4的两种情形分别画出剪拼成一个平行四边形的示意图．

联想拓展：
小明通过探究后发现：在一个四边形中，只要有一组对边平行，就可以剪拼成平行四边形．
如图5的多边形中，AE=CD，AE∥CD，能否象上面剪切方法一样沿一条直线进行剪切，拼成一个平行四边形？若能，请你在图中画出剪拼的示意图并作必要的文字说明；若不能，简要说明理由．