
题目列表(包括答案和解析)
 6、如图,AD∥BC,BD平分∠ABC,且∠A=110°,则∠D=
6、如图,AD∥BC,BD平分∠ABC,且∠A=110°,则∠D=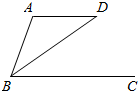 如图,AD∥BC,BD平分∠ABC,且∠A=110°,则∠D的度数为( )
如图,AD∥BC,BD平分∠ABC,且∠A=110°,则∠D的度数为( )| A、70° | B、35° | C、55° | D、110° |
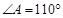 ,则
,则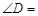
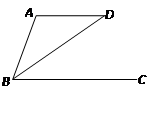
如图,AD∥BC,BD平分∠ABC,且![]() ,则
,则![]()
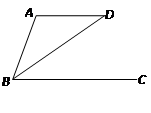
如图,AD∥BC,BD平分∠ABC,且∠A=110°,则∠D=_______度.
|

一、选择题(本题有10小题,每题4分,共40分)
1.B 2.A 3.D 4.A 5.C
6.D 7.B 8.C 9.C 10.A
二、填空题(本题有6小题,每题5分,共30分)
11.5.6 12.5
13. 14.
14.
15. 16.
16.
三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)
17.
 ????????????????????????????????????????????????????????????????????????????????????????????????? 6分
????????????????????????????????????????????????????????????????????????????????????????????????? 6分
 ?????????????????????????????????????????????????????????????????????????????????????????????????? 8分
?????????????????????????????????????????????????????????????????????????????????????????????????? 8分
18.
 ??????????????????????????????????????????????????????????????????????????????????? 6分
??????????????????????????????????????????????????????????????????????????????????? 6分
 ????????????????????????????????????????????????????????????????????????????????????????????????????? 8分
????????????????????????????????????????????????????????????????????????????????????????????????????? 8分
19.设 (度),则
(度),则 ,
, .
.
根据四边形内角和定理得, . ???????????????????????????????????? 4分
. ???????????????????????????????????? 4分
解得, .
.
∴ ,
, ,
, . ???????????????????????????????????????????????????????????????? 8分
. ???????????????????????????????????????????????????????????????? 8分
20.(1)B机器的产量为150件, ???????????????????????????????????????????????????????????????????????????? 2分
A机器的产量约为210件. ???????????????????????????????????????????????????????????????????????? 4分
(2)C机器产量的百分比为40%. ?????????????????????????????????????????????????????????????????????? 6分
设C机器的产量为x,
由 ,得
,得 ,即C机器的产量为240件. ???????????????????????????????? 8分
,即C机器的产量为240件. ???????????????????????????????? 8分
21.

(1)∵AE⊥BC,AF⊥CD,∴∠AEB=∠AFD=90°. ??????????????????????????????????????????????? 2分
∵四边形ABCD是平行四边形,∴∠ABE=∠ADF. ?????????????????????????????????????? 4分
∴△ABE∽△ADF ??????????????????????????????????????????????????????????????????????????????????? 5分
(2)∵△ABE∽△ADF,
∴∠BAG=∠DAH.
∵AG=AH,∴∠AGH=∠AHG,
从而∠AGB=∠AHD.
∴△ABG≌△ADH. ????????????????????????????????????????????????????????????????????????????????????????? 8分
∴ .
.
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形. ?????????????????????????????????????????????????????????????????? 10分
22.(1)∵ 都是正整数,且
都是正整数,且 ,∴
,∴ .
.
∴ ,
, ,
, ,
, ??????????????????????????????????????????????????????????????? 4分
??????????????????????????????????????????????????????????????? 4分
(2)从 ,
, ,
, ,
, 中任取两点作直线为:
中任取两点作直线为:
 ,
, ,
, ,
, ,
, ,
, .
.
∴不同的直线共有6条. ??????????????????????????????????????????????????????????????????????????????????? 9分
(3)∵只有直线 ,
, 与抛物线有公共点,
与抛物线有公共点,
∴从(2)的所有直线中任取一条直线与抛物线有公共点的概率是 ?????????? 12分
?????????? 12分
23.(1)由 ,解得
,解得 ,所以
,所以 ?????????????????????????????????????????? 4分
?????????????????????????????????????????? 4分
(2) ,
, .
.
在 △OCD中,
△OCD中, ,
, ,
,
∴
 . ???????????????????????????????????????????????????????????????????????????????? 8分
. ???????????????????????????????????????????????????????????????????????????????? 8分
(3)取点A关于原点的对称点 ,则问题转化为求证
,则问题转化为求证 .
.

由勾股定理可得,
 ,
, ,
, ,
,
∵ ,
,
∴△EOB是等腰直角三角形.
∴ .
.
∴ .??????????????????????????????????????????????????????????????????????????????????????????? 12分
.??????????????????????????????????????????????????????????????????????????????????????????? 12分
24.(1)在△ABC中,∵ ,
, ,
, .
.
∴ ,解得
,解得 . ????????????????????????????????????????????????????????????????? 4分
. ????????????????????????????????????????????????????????????????? 4分
(2)①若AC为斜边,则 ,即
,即 ,无解.
,无解.
②若AB为斜边,则 ,解得
,解得 ,满足
,满足 .
.
③若BC为斜边,则 ,解得
,解得 ,满足
,满足 .
.
∴ 或
或 . ??????????????????????????????????????????????????????????????????????????????????????????? 9分
. ??????????????????????????????????????????????????????????????????????????????????????????? 9分
(3)在△ABC中,作 于D,设
于D,设 ,△ABC的面积为S,则
,△ABC的面积为S,则 .
.

①若点D在线段AB上,则 .
.
∴ ,即
,即 .
.
∴ ,即
,即 .
.
∴
 (
( ). ?????????????????? 11分
). ?????????????????? 11分
当 时(满足
时(满足 ),
), 取最大值
取最大值 ,从而S取最大值
,从而S取最大值 .?????????? 13分
.?????????? 13分
②若点D在线段MA上,则 .
.

同理可得,
 (
( ),
),
易知此时 .
.
综合①②得,△ABC的最大面积为 ???????????????????????????????????????????????????????????? 14分
???????????????????????????????????????????????????????????? 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com