
题目列表(包括答案和解析)
探究:
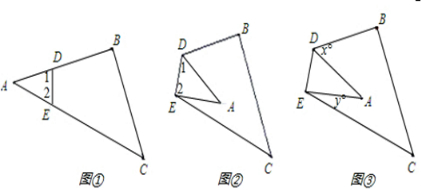
(1)如图①,∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,填空:∠1+∠2 ∠B+∠C(填“>”“<”“=”),当∠A=40°时,∠B+∠C+∠1+∠2= ;
(3)如图③,是由图①的△ABC沿DE折叠得到的,如果∠A=30°,则x+y=360°﹣(∠B+∠C+∠1+∠2)=360°﹣ = ,猜想∠BDA+∠CEA与∠A的关系为 .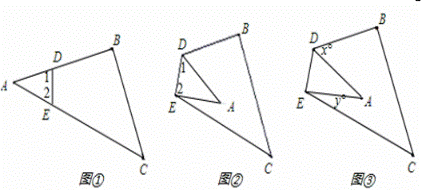
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com