
题目列表(包括答案和解析)
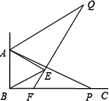
如图,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连接AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连接QE并延长交射线BC于点F.在下列结论中:①∠QFC=60°;②△AEQ≌△ABP;③BF=EF;④若线段AB=2![]() ,设BP=x,点Q到射线BC的距离为y,则y=
,设BP=x,点Q到射线BC的距离为y,则y=![]() x+
x+![]() (x>0).其中一定正确的结论个数有
(x>0).其中一定正确的结论个数有
A.1个
B.2个
C.3个
D.4个
已知:如图,在直角梯形ABCD中,AD∥BC,BC=5,CD=6,∠DCB=60°,∠ABC=90°.等边三角形MPN(N为不动点)的边长为a,边MN和直角梯形ABCD的底边BC都在直线l上,NC=8.将直角梯形ABCD向左翻折180°,翻折一次得到图形①,翻折二次得到图形②,如此翻折下去.

(1)求直角梯形ABCD的面积;
(2)将直角梯形ABCD向左翻折二次,如果此时等边三角形的边长a≥2,请直接写出这时两图形重叠部分的面积是多少?
(3)将直角梯形ABCD向左翻折三次,如果第三次翻折得到的直角梯形与等边三角形重叠部分的面积等于直角梯形ABCD的面积,请直接写出这时等边三角形的边长a至少应为多少?
已知Rt△ABC,∠ACB=90°,AC=BC=4,点O是AB中点,点P、Q分别从点A、C出发,沿AC、CB以每秒1个单位的速度运动,到达点C、B后停止.连结PQ、点D是PQ中点,连结CD并延长交AB于点E.
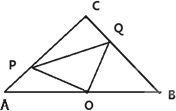
(1)试说明:△POQ是等腰直角三角形;
(2)设点P、Q运动的时间为t秒,试用含t的代数式来表示△CPQ的面积S,并求出S的最大值;
(3)如下图,点P在运动过程中,连结EP、EQ,问四边形PEQC是什么四边形,并说明理由;

(4)求点D运动的路径长(直接写出结果).
如图,已知AD是△ABC的中线,∠ADC=45°,把△ABC沿AD对折,点C落在点E的位置,连接BE,若BC=6cm。

(1)求BE的长;
(2)当AD=4cm时,求四边形BDAE的面积。
【解析】(1)由折叠可知:△ADC≌△ADE,∠EDC=2∠ADC=90°,ED=DC,又BD=DC,△BDE是等腰直角三角形,可求BE长;
(2)由(1)知,∠BED=45°,∠EDA=45°,∴四边形BDAE是梯形,已知上底AD=4,下底BE=3 2,为求梯形高,过D作DF⊥BE于点F,DF实际上就是等腰直角三角形BDE斜边上的高,可求长度.
如图所示,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下五个结论:
①AE=CF ②∠APE=∠CPF ③△EPF是等腰直角三角形 ④EF=AP ⑤S四边形AEPF=![]() .当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的序号有________.
.当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的序号有________.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com