
题目列表(包括答案和解析)
已知:在△ABC中,∠CAB=![]() ,且
,且![]() ,AP平分∠CAB.
,AP平分∠CAB.
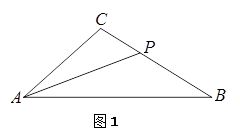
1.如图1,若![]() ,∠ABC=32°,且AP交BC于点P,试探究线段
,∠ABC=32°,且AP交BC于点P,试探究线段
AB,AC与PB之间的数量关系,并对你的结论加以证明;
答:线段AB,AC与PB之间的数量关系为:___________________________.
2.如图2,若∠ABC=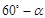 ,点P在△ABC的内部,且使∠CBP=30°,
,点P在△ABC的内部,且使∠CBP=30°,
求∠APC的度数(用含![]() 的代数式表示)
的代数式表示)

已知:在△ABC中,∠CAB=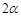 ,且
,且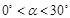 ,AP平分∠CAB.
,AP平分∠CAB.
1.如图1,若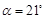 ,∠ABC=32°,且AP交BC于点P,试探究线段
,∠ABC=32°,且AP交BC于点P,试探究线段
AB,AC与PB之间的数量关系,并对你的结论加以证明;
答:线段AB,AC与PB之间的数量关系为:___________________________.
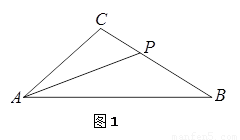
2.如图2,若∠ABC= ,点P在△ABC的内部,且使∠CBP=30°,
,点P在△ABC的内部,且使∠CBP=30°,
求∠APC的度数(用含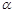 的代数式表示)
的代数式表示)
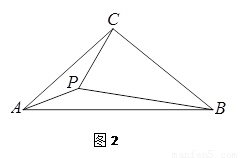
已知:在△ABC中,∠CAB=![]() ,且
,且![]() ,AP平分∠CAB.
,AP平分∠CAB.
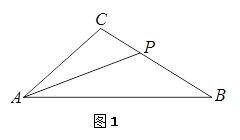
1.(1)如图1,若![]() ,∠ABC=32°,且AP交BC于点P,试探究线段
,∠ABC=32°,且AP交BC于点P,试探究线段
AB,AC与PB之间的数量关系,并对你的结论加以证明;
答:线段AB,AC与PB之间的数量关系为:___________________________.
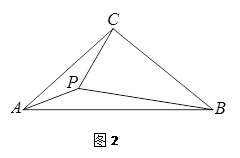
2.(2)如图2,若∠ABC=![]() ,点P在△ABC的内部,且使∠CBP=30°,
,点P在△ABC的内部,且使∠CBP=30°,
求∠APC的度数(用含![]() 的代数式表示).
的代数式表示).
已知:在△ABC中,∠CAB=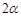 ,且
,且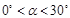 ,AP平分∠CAB.
,AP平分∠CAB.
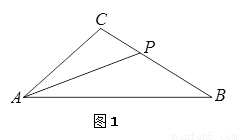
1.(1)如图1,若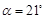 ,∠ABC=32°,且AP交BC于点P,试探究线段
,∠ABC=32°,且AP交BC于点P,试探究线段
AB,AC与PB之间的数量关系,并对你的结论加以证明;
答:线段AB,AC与PB之间的数量关系为:___________________________.
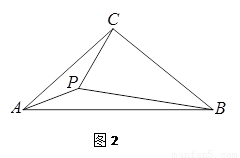
2.(2)如图2,若∠ABC=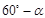 ,点P在△ABC的内部,且使∠CBP=30°,
,点P在△ABC的内部,且使∠CBP=30°,
求∠APC的度数(用含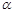 的代数式表示).
的代数式表示).
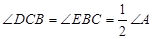 ,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.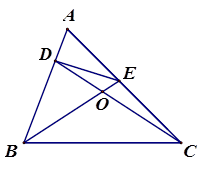
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com