
题目列表(包括答案和解析)
已知![]() 均为正数,
均为正数,![]() ,则
,则![]() 的最小值是 ( )
的最小值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷 (非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分,将答案填在题中的横线上。
设  ,则
,则 的最大值.为( )
的最大值.为( )
A. B.
B. C. D.
C. D.
第II卷(非选择题 共70分)
已知 ,且
,且 ,则 ( )
,则 ( )
A.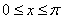 B.
B.
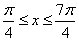
C.  D.
D.

第II卷(非选择题,共60分)
正项数列![]() 的前n项的乘积
的前n项的乘积![]() ,则数列
,则数列![]() 的前n项和
的前n项和![]() 中的最大值是 ( )
中的最大值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题,共90分)
设函数![]() ,则满足方程
,则满足方程![]() 根的个数是( )
根的个数是( )
A.1 个 B.2 个 C.3 个 D.无数个
第Ⅱ卷 非选择题(共100分)
|