
题目列表(包括答案和解析)
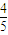 、
、 、
、 (允许小张被多个单位同时录用).
(允许小张被多个单位同时录用).大学毕业的小张到甲、乙、丙三个单位应聘,各单位是否录用他相互独立,其被录用的概率分别为![]() 、
、![]() 、
、![]() (允许小张被多个单位同时录用).
(允许小张被多个单位同时录用).
(1)小张没有被录用的概率;
(2)求小张被2个单位同时录用的概率;
(3)设没有录用小张的单位个数为ξ,求ξ的分布列和它的数学期望.
大学毕业生小张到甲、乙、丙三个单位应聘,各单位是否录用他是相互独立的,其被录用的概率分别为![]() ,
,![]() ,
,![]() (允许小张被多个单位同时录用),
(允许小张被多个单位同时录用),
(1)求小张没有被录用的概率;
(2)求小张恰被两个单位录用的概率。
(1)求小张没有被录用的概率;
(2)求小张恰被三个单位录用的概率;
(理)(3)设录用小张的单位个数为ξ,求ξ的分布列和它的数学期望.
| 4 |
| 5 |
| 2 |
| 3 |
| 3 |
| 4 |
|