
题目列表(包括答案和解析)
(本小题满分10分)如图,已知反比例函数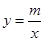 (
(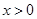 )的图象与一次函数
)的图象与一次函数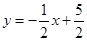 的图象交于
的图象交于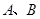 两点,点
两点,点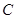 的坐标为
的坐标为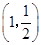 ,连接
,连接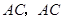 平行于
平行于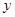 轴.
轴.
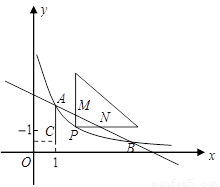
(1)求反比例函数的解析式及点 的坐标.
的坐标.
(2)现有一个直角三角板,让它的直角顶点 在反比例函数图象上的
在反比例函数图象上的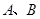 之间的部分滑动(不与
之间的部分滑动(不与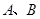 重合),两直角边始终分别平行于
重合),两直角边始终分别平行于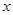 轴、
轴、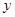 轴,且与线段
轴,且与线段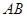 交于
交于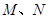 两点,试判断
两点,试判断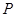 点在滑动过程中
点在滑动过程中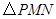 是否与
是否与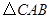 总相似,简要说明判断理由.
总相似,简要说明判断理由.
(本小题满分10分)如图,在平面直角坐标系中,点A、B、C、P的坐标分别为(0,1)、(-1,0)、(1,0)、(-1,-1)。
【小题1】(1)求经过A、B、C三点的抛物线的表达式;
【小题2】(2)以P为位似中心,将△ABC放大,使得放大后的△A1B1C1与△OAB对应线段的比为3:1,请在右图网格中画出放大后的△A1B1C1;(所画△A1B1C1与△ABC在点P同侧);
【小题3】(3)经过A1、B1、C1三点的抛物线能否由(1)中的抛物线平移得到?请说明理由。
(本小题满分10分)如图,在平面直角坐标系中,点A、B、C、P的坐标分别为(0,1)、(-1,0)、(1,0)、(-1,-1)。
【小题1】(1)求经过A、B、C三点的抛物线的表达式;
【小题2】(2)以P为位似中心,将△ABC放大,使得放大后的△A1B1C1
与△OAB对应线段的比为3:1,请在右图网格中画出放大
后的△A1B1C1;(所画△A1B1C1与△ABC在点P同侧);
【小题3】(3)经过A1、B1、C1三点的抛物线能否由(1)中的抛物线平
移得到?请说明理由。
(本小题满分10分)
如图14①至图14④中,两平行线AB、CD音的距离均为6,点M为AB上一定点.
思考:如图14①中,圆心为O的半圆形纸片在AB、CD之间(包括AB、CD),其直径MN在AB上,MN=8,点P为半圆上一点,设∠MOP=α,当α=________度时,点P到CD的距离最小,最小值为____________.
探究一在图14①的基础上,以点M为旋转中心,在AB、CD之间顺时针旋转该半圆形纸片,直到不能再转动为止.如图14②,得到最大旋转角∠BMO=_______度,此时点N到CD的距离是______________.
探究二将图14①中的扇形纸片NOP按下面对α的要求剪掉,使扇形纸片MOP绕点M在AB、CD之间顺时针旋转.
⑴如图14③,当α=60°时,求在旋转过程中,点P到CD的最小距离,并请指出旋转角∠BMO的最大值:
⑵如图14④,在扇形纸片MOP旋转过程中,要保证点P能落在直线CD上,请确定α的取值范围.
(参考数据:sin49°= ,cos41°=
,cos41°= ,tan37°=
,tan37°= )
)


(本小题满分10分)
如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D,∠B = 30°.
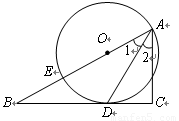
求证:1.(1)AD平分∠BAC,2.(2)若BD = 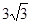 ,求B E的长.
,求B E的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com