
题目列表(包括答案和解析)
在一个不透明的口袋里装有四个分别标有
1、2、3、4的小球,它们的形状、大小等完全相同.小明先从口袋里随机不放回地取出一个小球,记下数字为x;小红在剩下有三个小球中随机取出一个小球,记下数字y.(1)计算由x、y确定的点(x,y)在函数y=-x+6图象上的概率;
(2)小明、小红约定做一个游戏,其规则是:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜.这个游戏规则公平吗?说明理由;若不公平,怎样修改游戏规则才对双方公平?
从-![]() ,-
,-![]() ,
,![]() ,
,![]() 这四个数中任取两个不同的数作为一次函数
这四个数中任取两个不同的数作为一次函数![]() +
+![]() 的一次项系数
的一次项系数![]() 和常数项
和常数项![]() .
.
(1)易用树状图(或列表法)表示![]() 、
、![]() 所有可能出现的结果
所有可能出现的结果
(2)中求出使得一次函数![]() +
+![]() 图象不经过第三象限的概率.
图象不经过第三象限的概率.
有A、B两个不透明的布袋,A袋中有两个完全相同的小球,分别标有数字0和-2;B袋中有三个完全相同的小球,分别标有数字-2、0和1.小明从A袋中随机取出一个小球,记录标有的数字为x,再从B袋中随机取出一个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
(1)写出点Q所有可能的坐标;
(2)求点Q在x轴上的概率;
(3)在平面直角坐标系xOy中,⊙O的半径是2,求过点Q能作⊙O切线的概率.
如图,在等腰梯形ABCD中,AD∥BC,AB=DC=50,AD=75,BC=135.点P从点B出发沿折线段BA-AD-DC以每秒5个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动,过点Q向上作射线QK⊥BC,交折线段CD-DA-AB于点E.点P、Q同时开始运动,当点P与点C重合时停止运动,点Q也随之停止,设点P、Q运动的时间是t秒(t>0).
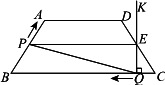
(1)当点P到达终点C时,求t的值,并指出此时BQ的长;
(2)当点P运动到AD上时,t为何值能使PQ∥DC?
(3)设射线QK扫过梯形ABCD的面积为S,分别求出点E运动到CD、DA上时,S与t的函数关系式;(不必写出t的取值范围)
(4)△PQE能否成为直角三角形?若能,写出t的取值范围;若不能,请说明理由.
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”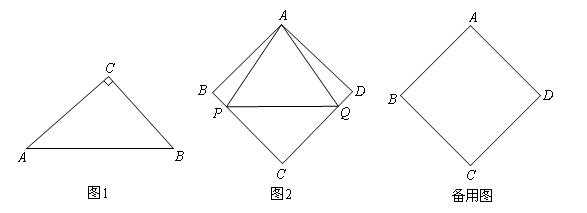
(1)请用直尺与圆规画一个“好玩三角形”;
(2)如图1,在Rt△ABC中,∠C=90°,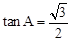 ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”;
(3)如图2,已知菱形ABCD的边长为a, ∠ABC=2β,点P,Q从点A同时出发,以相同的速度分别沿折线AB-BC和AD-DC向终点C运动,记点P所经过的路程为s
①当β=45°时,若△APQ是“好玩三角形”,试求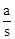 的值;
的值;
②当tanβ的取值在什么范围内,点P,Q在运动过程中,有且只有一个△APQ能成为“好玩三角形”?请直接写出tanβ的取值范围。
(4)本小题为选做题
依据(3)中的条件,提出一个关于“在点P,Q的运动过程中,tanβ的取值范围与△APQ是“好玩三角形”的个数关系”的真命题(“好玩三角形”的个数限定不能为1)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com