题目列表(包括答案和解析)
某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验如下：
|
零件的个数 |
2 |
3 |
4 |
5 |
|
加工的时间 |
2.5 |
3 |
4 |
4.5 |
（1）在给定坐标系中画出表中数据的散点图；
（2）求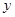
关于
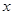的线性回归方程
；
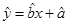（3）试预测加工10个零件需要多少时间？
（
，
）
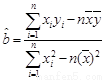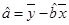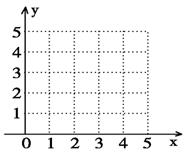
【解析】第一问中，利用表格中的数据先作出散点图
第二问中，求解均值a,b的值，从而得到线性回归方程。
第三问，利用回归方程将x=10代入方程中，得到y的预测值。
解：（1）散点图（略） (2分)
（2）
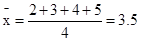
（4分）
∴
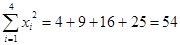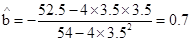(7分)
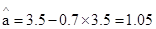(8分)∴回归直线方程：
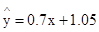(9分)
(3)当
∴预测加工10个零件需要8.05小时。
|
例10．（2004年重庆卷）某工厂生产某种产品，已知该产品的月生产量（吨）与每吨产品的价格（元/吨）之间的关系式为：,且生产x吨的成本为（元）.问该厂每月生产多少吨产品才能使利润达到最大？最大利润是多少？（利润=收入─成本）
解：每月生产x吨时的利润为
，故它就是最大值点，且最大值为：
答：每月生产200吨产品时利润达到最大，最大利润为315万元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com