
题目列表(包括答案和解析)
如图所示,有一电子束从点a处以一定的水平速度飞向竖直放置的荧光屏,将垂直击中荧光屏上的点b,已知电子的质量为m,电量为q.
(1)若在电子束运行途中加一半径为R的圆形磁场,磁感应强度为B,方向垂直于纸面向里,圆心O在点a、b连线上,点O距荧光屏距离为L,为使电子束仍击中荧光屏上的点b,可加一个场强为E的匀强电场,指出此匀强电场的方向和范围,并求出电子束的速度.
(2)现撤去电场,电子束以原速度沿原来方向从a点发射,运动方向在磁场中偏转后击中荧光屏上的点c.求b、c间的距离.


如图所示,有一电子束从点a处以一定的水平速度飞向竖直放置的荧光屏,将垂直击中荧光屏上的点b,已知电子的质量为m,电量为a.
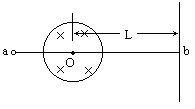
①若在电子束运行途中经一半径为R的圆形磁场,磁感应强度为B,方向垂直于纸面向里,圆心O在点a、b连线上,点O距荧光屏距离为L,为使电子束仍击中荧光屏上的点b,可加一个场强为E的匀强电场,指出此匀强电场的方向和范围,并求出电子束的速度.
②现撤去电场,电子束以原速度沿原来方向从a点发射,运动方向在磁场中偏转后击中荧光屏上的点C.求b、c间的距离.
如图所示,有一电子束从点a处以一定的水平速度飞向竖直放置的荧光屏,将垂直击中荧光屏上的点b,已知电子的质量为m,电量为e.
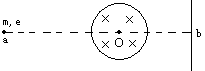
(1)若在电子束运行途中加一半径为R的圆形磁场,磁感应强度为B,方向垂直纸面向里,圆心O在点a,b连线上,点O距荧光屏距离为L,为使电子仍击中荧光屏上的点b,可加一个场强为E的匀强电场,指出此匀强电场的方向和范围,并求出电子束的速度.
(2)现撤去电场,电子束以原速度沿原来方向从a点发射,运动方向在磁场中偏转后击中荧光屏上的点c,求b,c间的距离.
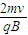 ,内半径为
,内半径为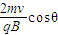
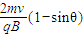
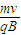 (1+sinθ)
(1+sinθ)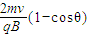
一、1、C2、C 3、B 4、C 5、BC 6、B 7、AD 8、D
二、实验题:(18分)将答案填在题目的空白处,或者要画图连线。
9、(6分)__BE_ (3分) ____AD___(3分)
10、(12分)(1)如图b(4分)
(2)由于RL2比RL1小得多,灯泡L2分得的电压很小,虽然有电流渡过,但功率很小,不能发光。(4分)
(3)如图c
解析:由于灯泡L2和L1额定电压相同,灯泡L2功率大得多,故RL2比RL1小得多,灯泡L2分得的电压很小,虽然有电流渡过,但功率很小,不能发光。(4分)
三、本大题共三小题共计54分.解答时请写出必要的文字说明、方程式和重要的演算步骤.只写出最后答案的不能得分.有数值计算的题.答案中必须明确写出数值和单位
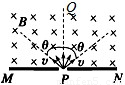
11、(16分)(1) 根据带电小球A恰能做完整的圆周运动,因 ,则小球能通过复合场中的最高点P(如图)设经过轨道上的P点的速度为v,由小球A的重力和电场力的合力提供向心力有:
,则小球能通过复合场中的最高点P(如图)设经过轨道上的P点的速度为v,由小球A的重力和电场力的合力提供向心力有:
在圆周轨道的最低点弹簧将B、A两球向左、右弹开,设弹开时A、B两球的速度大小分别为vA、vB,由动量守恒有:
小球A从圆周轨道的最低点运动到P的过程中,由动能定理有:
(2)设BC碰后速度为v1 , B与C碰撞动量守恒
BC整体减速,D球加速,当两者速度相等时设为v2,弹簧最短,弹性势能最大
12、(18分)(1)(6分)设球到D点时的速度为 ,从释放至D点,
,从释放至D点,
根据动能定理 (3分)
(3分)
对 球,根据动量守恒定律
球,根据动量守恒定律  (2分)
(2分)
解得 (1分)
(1分)
(2)(6分)两球进入复合场后,由计算可知 两球在洛伦兹力作用下做匀速圆周运动,轨迹示意图如右图所示(1分)
两球在洛伦兹力作用下做匀速圆周运动,轨迹示意图如右图所示(1分)
 洛伦兹力提供向心力
洛伦兹力提供向心力 (2分)
(2分)
由图可知 (2分)
(2分)
解得 (1分)
(1分)
(3)(6分) 系统损失的机械能
系统损失的机械能

或
解得
13、(20分)⑴设匀速直线运动的速度为v0, ef有效切割长度为l,则电流:
 ,由于v0不变,所以I不变。或由平衡条件证明同样给分(4分)
,由于v0不变,所以I不变。或由平衡条件证明同样给分(4分)
⑵由能量守恒,得:… ………………………(2分)
………………………(2分)
设弹簧形变量为x,由平衡条件,得: 2BIxtan30°= kx…………(2分)
解得 v0 = (2分) k = …(2分)
⑶ef越过O点后,与弹簧脱离,设导体棒最终停止位置距O点的距离为x0,某时刻回路中ef有效切割长度为L1,ef的速度为v,加速度为a,电流为I, 据牛顿第二定律,得:― BIL1= ma
电流 I = = 得: ― = ma……………………… (3分)
取一小段时间△t,速度微小变化为△v,回路面积微小增加为△S,则 ― △t = ma△t
即: ― ∑△t = ∑ma△t ―∑L1v△t = m∑a△t ―∑△S = m∑△v
― x02tan300= 0-mv0 (3分) 将 v0= 代入,得:x 0 = ―― (2分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com