
题目列表(包括答案和解析)
C.选修4-4:坐标系与参数方程
在极坐标系下,已知圆O: 和直线
和直线 ,
,
(1)求圆O和直线 的直角坐标方程;(2)当
的直角坐标方程;(2)当 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
D.选修4-5:不等式证明选讲
对于任意实数
 和
和 ,不等式
,不等式 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
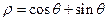 和直线
和直线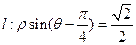 ,
, 的直角坐标方程;(2)当
的直角坐标方程;(2)当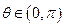 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.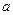
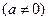 和
和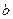 ,不等式
,不等式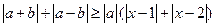 恒成立,试求实数
恒成立,试求实数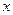 的取值范围.
的取值范围.C
[解析] 由基本不等式,得ab≤![]() =
=![]() =
=![]() -ab,所以ab≤
-ab,所以ab≤![]() ,故B错;
,故B错;![]() +
+![]() =
=![]() =
=![]() ≥4,故A错;由基本不等式得
≥4,故A错;由基本不等式得![]() ≤
≤![]() =
=![]() ,即
,即![]() +
+![]() ≤
≤![]() ,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×
,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×![]() =
=![]() ,故D错.故选C.
,故D错.故选C.
.定义域为R的函数 满足
满足 ,且当
,且当 时,
时, ,则当
,则当 时,
时, 的最小值为( )
的最小值为( )
(A) (B)
(B) (C)
(C) (D)
(D)
.过点 作圆
作圆 的弦,其中弦长为整数的共有 ( )
的弦,其中弦长为整数的共有 ( )
A.16条 B. 17条 C. 32条 D. 34条
数学(理)
第I卷(共60分)
一、选择题(每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
C
C
A
A
A
A
D
B
A
A
第Ⅱ卷(共90分)
二、填空题(每小题4分,共16分)
13..files/image298.gif) 14.3 15.97 16.③
14.3 15.97 16.③
三、解答题(共74分)
17.(本小题满分12分)
(I).files/image225.gif) 的内角和
的内角和.files/image301.gif) 。
。
.files/image303.gif) ,
,
.files/image305.gif)
(Ⅱ).files/image307.gif)
.files/image309.gif)
当.files/image311.gif) 即
即.files/image313.gif) 时,
时,.files/image092.gif) 取最大值
取最大值.files/image316.gif)
18.(本题满分12分)
记A:该夫妇生一个小孩是患病男孩,B:该夫妇生一个小孩是患病女孩:C:该夫妇生一个小孩是不患病男孩;D:该夫妇生一个小孩是不患病女孩,则
.files/image318.gif)
(I).files/image320.gif)
.files/image322.gif)
.files/image324.gif)
(Ⅱ)显然,.files/image244.gif) 的取值为0,1,2,3
的取值为0,1,2,3
.files/image327.gif)
.files/image329.gif)
所以.files/image244.gif) 的分布列为
的分布列为
.files/image244.gif)
0
1
2
3
.files/image013.gif)
.files/image334.gif)
.files/image336.gif)
.files/image338.gif)
.files/image340.gif)
显然,.files/image342.gif) ,故
,故.files/image344.gif)
19.(本题满分12分)
解法一:(I)证明:连接.files/image346.gif) ,设
,设.files/image348.gif) ,连接DE
,连接DE
.files/image350.gif) 三棱柱
三棱柱.files/image249.gif) 是正三棱柱,且
是正三棱柱,且.files/image255.gif) ,
,
.files/image354.gif) 四边形
四边形.files/image356.gif) 是正方形,
是正方形,
∴E是.files/image346.gif) 的中点,又
的中点,又.files/image251.gif) 是
是.files/image253.gif) 的中点,
的中点,
∴.files/image361.gif)
∵.files/image363.gif) 平面
平面.files/image365.gif) 平面
平面.files/image259.gif) ,
,
∴.files/image257.gif) 平面
平面.files/image259.gif)
(Ⅱ)解:在平面.files/image370.gif) 内作
内作.files/image372.gif) 于点
于点.files/image374.gif) ,在面
,在面.files/image376.gif) ;内作
;内作.files/image378.gif) 于
于.files/image380.gif) 连接
连接.files/image382.gif) 。
。
∵平面.files/image384.gif) 平面
平面.files/image370.gif) ,∴
,∴.files/image387.gif) 平面
平面.files/image356.gif) ,
,
∵.files/image390.gif) 是
是.files/image382.gif) 在平面
在平面.files/image356.gif) 上的射影,
上的射影,.files/image394.gif)
∴.files/image396.gif) 是二面角
是二面角.files/image261.gif) 的平面角
的平面角
设.files/image399.gif) 在正
在正.files/image225.gif) 中,
中,.files/image402.gif)
在.files/image404.gif) 中,
中,.files/image406.gif) 在
在.files/image408.gif) 中,
中,.files/image410.gif)
从而.files/image412.gif)
所以,二面角.files/image261.gif) 的平面角的余弦值为
的平面角的余弦值为.files/image415.gif)
解法二:建立空间直角坐标系.files/image417.gif) ,如图,
,如图,
(I)证明:连接.files/image419.gif) 设
设.files/image421.gif) ,连接
,连接.files/image423.gif) ,设
,设.files/image425.gif)
.files/image427.jpg) 则
则.files/image429.gif)
.files/image431.gif)
.files/image433.gif)
.files/image435.gif) 平面
平面.files/image365.gif) 平面
平面.files/image438.gif) 平面
平面.files/image259.gif)
(Ⅱ)解:∵.files/image441.gif)
设.files/image443.gif) 是平面
是平面.files/image259.gif) 的法向量,则
的法向量,则.files/image446.gif) ,且
,且.files/image448.gif)
故.files/image450.gif) ,取
,取.files/image452.gif) ,得
,得.files/image454.gif) ;
;
同理,可求得平面.files/image456.gif) 的法向量是
的法向量是.files/image458.gif)
设二面角.files/image261.gif) 的大小为
的大小为.files/image461.gif) ,则
,则.files/image463.gif)
所以,二面角.files/image261.gif) 的平面角的余弦值为
的平面角的余弦值为.files/image415.gif)
20.(本题满分12分)
(I).files/image467.gif)
.files/image469.gif) 在
在.files/image265.gif) 上是增函数,
上是增函数,
.files/image472.gif) 在
在.files/image265.gif) 上恒成立,即
上恒成立,即.files/image475.gif) 恒成立。
恒成立。
.files/image477.gif) (当且仅当
(当且仅当.files/image479.gif) 时,等号成立),
时,等号成立),
.files/image481.gif)
所以.files/image483.gif)
(Ⅱ)设.files/image485.gif) ,则
,则.files/image487.gif)
.files/image489.gif)
(1)当.files/image491.gif) 时,
时,.files/image493.gif) 最小值为
最小值为.files/image495.gif) ;
;
(2)当.files/image497.gif) 时,
时,.files/image493.gif) 最小值为
最小值为.files/image500.gif)
21.(本题满分12分)
(I)将.files/image274.gif) 代入
代入.files/image503.gif) 得
得.files/image505.gif) ,整理得
,整理得
.files/image507.gif)
由.files/image509.gif) 得
得.files/image511.gif) ,故
,故
.files/image513.gif)
(Ⅱ)当两条切线的斜率都存在而且不等于.files/image515.gif) 时,设其中一条的斜率为k,
时,设其中一条的斜率为k,
则另外一条的斜率为.files/image517.gif)
于是由上述结论可知椭圆斜率为k的切线方程为
.files/image519.gif) ①
①
又椭圆斜率为.files/image517.gif) 的切线方程为
的切线方程为
.files/image522.gif) ②
②
由①得.files/image524.gif)
由②得.files/image526.gif)
两式相加得.files/image528.gif)
于是,所求P点坐标.files/image530.gif) 满足
满足.files/image532.gif) 因此,
因此,.files/image534.gif)
当一条切线的斜率不存在时,另一条切线的斜率必为0,此时显然也有.files/image534.gif)
所以.files/image537.gif) 为定值。
为定值。
22.(本题满分14分)
(I)由.files/image539.gif) 知
知.files/image541.gif)
当.files/image543.gif) 时,
时,.files/image545.gif) ,化简得
,化简得
.files/image547.gif) ①
①
以.files/image549.gif) 代替
代替.files/image015.gif) 得
得
.files/image552.gif) ②
②
两式相减得
.files/image554.gif)
则.files/image556.gif) ,其中
,其中.files/image543.gif)
所以,数列.files/image057.gif) 为等差数列
为等差数列
(Ⅱ)由.files/image560.gif) ,结合(I)的结论知
,结合(I)的结论知.files/image562.gif)
于是不等式.files/image564.gif)
因此,欲证原不等式成立,只需证.files/image566.gif) 即
即.files/image568.gif)
令.files/image570.gif) ,则
,则.files/image572.gif) 在
在.files/image574.gif) 上恒正,
上恒正,
.files/image576.gif) 在
在.files/image574.gif) 上单调递增,当
上单调递增,当.files/image579.gif) 时,恒有
时,恒有.files/image581.gif)
其他解法参照以上评分标准评分
本资料由《七彩教育网》www.7caiedu.cn 提供!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com