练习册

  • 练习册
  • 试题
    16．右图是求数列前10项中最大项的程序框图.①.②处分别应该填上 . . 【查看更多】

     

    题目列表(包括答案和解析)

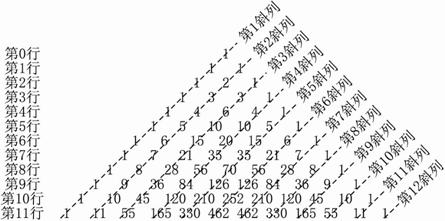
    杨辉是中国南宋末年的一位杰出的数学家、数学教育家.他的数学著作颇多,他编著的数学书共5种21卷,在他的著作中收录了不少现已失传的古代数学著作中的算题和算法.他的数学研究与教育工作的重点是在计算技术方面.杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴涵了许多优美的规律.古今中外,许多数学家如贾宪、朱世杰、帕斯卡、华罗庚等都曾深入研究过,并将研究结果应用于其他工作.下图是一个11阶的杨辉三角:

     

    试回答:(其中第(1)&(5)小题只需直接给出最后的结果,无需求解过程)

    (1)记第i(i∈N*)行中从左到右的第j(j∈N*)个数为aij,则数列{aij}的通项公式为          ,

    n阶杨辉三角中共有           个数;

    (2)第k行各数的和是;

    (3)n阶杨辉三角的所有数的和是;

    (4)将第n行的所有数按从左到右的顺序合并在一起得到的多位数等于;

    (5)第p(p∈N*,且p≥2)行除去两端的数字1以外的所有数都能被p整除,则整数p一定为(   )

    A.奇数                B.质数              C.非偶数                D.合数

    (6)在第3斜列中,前5个数依次为1、3、6、10、15;第4斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:

    第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数.

    试用含有m、k(m、k∈N*)的数学公式表示上述结论并证明其正确性.

    数学公式为                   .

    证明:                        .

    查看答案和解析>>

     

    一、选择题

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    答案

    D

    B

    A

    C

    A

    B

    D

    B

    D

    C

    A

    C

    二、填空题

    13．30°   14．6ec8aac122bd4f6e    15．-0.61    16．6ec8aac122bd4f6e

    三、解答题

    17．解：（I）6ec8aac122bd4f6e

           即6ec8aac122bd4f6e中出现3个1，2个0         2分

           所以6ec8aac122bd4f6e       6分

       （II）（法一）设Y=X-1，

           由题知6ec8aac122bd4f6e        9分

           所以6ec8aac122bd4f6e      12分

       （法二）X的分布列如下：

    X

    1

    2

    3

    4

    P（X）

    6ec8aac122bd4f6e

    6ec8aac122bd4f6e

    6ec8aac122bd4f6e

    6ec8aac122bd4f6e

    X

    5

    6

     

    P（X）

    6ec8aac122bd4f6e

    6ec8aac122bd4f6e

     

        ……10服

           所以6ec8aac122bd4f6e…………12分

    18．解：（I）由三视图可得，三棱锥A―BCD中

           6ec8aac122bd4f6e都等于90°，

           每个面都是直角三角形；

           可得6ec8aac122bd4f6e面ADB，所以6ec8aac122bd4f6e……2分

           又6ec8aac122bd4f6e，所以6ec8aac122bd4f6e面ABC，

           所以DE6ec8aac122bd4f6eAC，       4分

           又DF6ec8aac122bd4f6eAC，所以AC6ec8aac122bd4f6e面DEF。   6分

      

     

     

     

    （II）方法一：由（I）知6ec8aac122bd4f6e为二面角B―AC―D的平面角，    9分

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

           6ec8aac122bd4f6e

           6ec8aac122bd4f6e

           6ec8aac122bd4f6e   12分

           方法二：过B作6ec8aac122bd4f6eCD于O，

           过O作OM6ec8aac122bd4f6eAC于M，连结BM，

           因为AD6ec8aac122bd4f6e面BDC，所以ADC6ec8aac122bd4f6e面BDC。

           所以BO6ec8aac122bd4f6e面ADC，

           由三垂线定理可得6ec8aac122bd4f6e为二面角B―AC―D的平面角，   9分

           可求得6ec8aac122bd4f6e

           所以6ec8aac122bd4f6e，

           所以6ec8aac122bd4f6e       12分

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

     

     

    方法三：如图，以DB为x轴，

           过D作BC的不行线这y轴，DA为z轴建立空间直角坐标系。

           所以6ec8aac122bd4f6e      8分

           设面DAC的一个法向量为6ec8aac122bd4f6e，

           则6ec8aac122bd4f6e

           则6ec8aac122bd4f6e

           设面BAC的一个法向量为6ec8aac122bd4f6e，

           则6ec8aac122bd4f6e

           则6ec8aac122bd4f6e       10分

           所以6ec8aac122bd4f6e，

           因为二面角B―AC―D为锐角，

           所以二面角B―AC―D的大小为6ec8aac122bd4f6e       12分

    19．解：（Ⅰ）设动点M的坐标为

    6ec8aac122bd4f6e，

           6ec8aac122bd4f6e

           即6ec8aac122bd4f6e………………2分

       （Ⅱ）①在6ec8aac122bd4f6e中分别令

           6ec8aac122bd4f6e……………3分

    设6ec8aac122bd4f6e，

    由6ec8aac122bd4f6e

           6ec8aac122bd4f6e………………4分

           6ec8aac122bd4f6e，

           所以6ec8aac122bd4f6e

           即6ec8aac122bd4f6e

           6ec8aac122bd4f6e………………6分

           ②6ec8aac122bd4f6e

                                    6ec8aac122bd4f6e……………7分

    点N到CD的距离6ec8aac122bd4f6e……………8分

    6ec8aac122bd4f6e…………………9分

    6ec8aac122bd4f6e

           当且仅当6ec8aac122bd4f6e时等号成立，

           即6ec8aac122bd4f6e，此时6ec8aac122bd4f6e，

    所以直线的方程为6ec8aac122bd4f6e…………………12分

    20．证明：（I）先证6ec8aac122bd4f6e

           法一：6ec8aac122bd4f6e

           6ec8aac122bd4f6e

           6ec8aac122bd4f6e

           法二：①6ec8aac122bd4f6e；

           ②假设6ec8aac122bd4f6e时命题成立，

           即6ec8aac122bd4f6e

           所以6ec8aac122bd4f6e时命题也成立。

           综合①②可得6ec8aac122bd4f6e      2分

           再证6ec8aac122bd4f6e

           ①6ec8aac122bd4f6e；

           ②假设6ec8aac122bd4f6e时命题成立，即6ec8aac122bd4f6e，

           则6ec8aac122bd4f6e

           6ec8aac122bd4f6e

           6ec8aac122bd4f6e

           所以6ec8aac122bd4f6e时命题也成立。

           综合①②可得6ec8aac122bd4f6e         6分

       （II）6ec8aac122bd4f6e

           6ec8aac122bd4f6e

           6ec8aac122bd4f6e

           故数列6ec8aac122bd4f6e单调递减             9分

           6ec8aac122bd4f6e

           6ec8aac122bd4f6e

           又6ec8aac122bd4f6e

           6ec8aac122bd4f6e

           即6ec8aac122bd4f6e       12分

    21．解：（I）因为6ec8aac122bd4f6e，所以

           方法一：6ec8aac122bd4f6e     2分

           因为6ec8aac122bd4f6e上是增函数，

           所以6ec8aac122bd4f6e上恒成立，

           即6ec8aac122bd4f6e上恒成立，

           所以6ec8aac122bd4f6e      4分

           又6ec8aac122bd4f6e存在正零点，

           故6ec8aac122bd4f6e。

           即6ec8aac122bd4f6e

           所以6ec8aac122bd4f6e       6分

           方法二：6ec8aac122bd4f6e     2分

           因为6ec8aac122bd4f6e上是增函数，

           所以6ec8aac122bd4f6e上恒成立，

           若6ec8aac122bd4f6e，

           于是6ec8aac122bd4f6e恒成立。

           又6ec8aac122bd4f6e存在正零点，

           故6ec8aac122bd4f6e

           6ec8aac122bd4f6e与6ec8aac122bd4f6e

           即6ec8aac122bd4f6e矛盾，

           所以6ec8aac122bd4f6e      4分

    由6ec8aac122bd4f6e恒成立，

    又6ec8aac122bd4f6e存在正零点，

    故6ec8aac122bd4f6e

    所以6ec8aac122bd4f6e即6ec8aac122bd4f6e       6分           

       （II）结论6ec8aac122bd4f6e理由如下：

           由（I），

           6ec8aac122bd4f6e

           所以6ec8aac122bd4f6e      7分

           方法一：6ec8aac122bd4f6e

           6ec8aac122bd4f6e

           6ec8aac122bd4f6e        8分

           令6ec8aac122bd4f6e

           6ec8aac122bd4f6e上，6ec8aac122bd4f6e

           所以6ec8aac122bd4f6e上为增函数         10分

           当6ec8aac122bd4f6e

           即6ec8aac122bd4f6e

           从而6ec8aac122bd4f6e得到证明。      12分

           方法二：

    6ec8aac122bd4f6e，

           6ec8aac122bd4f6e

           6ec8aac122bd4f6e       8分

           令6ec8aac122bd4f6e，

           作函数6ec8aac122bd4f6e

           令6ec8aac122bd4f6e

           当6ec8aac122bd4f6e       10分

           6ec8aac122bd4f6e，

           所以当6ec8aac122bd4f6e，

           即6ec8aac122bd4f6e

           所以6ec8aac122bd4f6e      12分

    22．证明：（I）6ec8aac122bd4f6e⊙O切BC于D，

           6ec8aac122bd4f6e       2分

           6ec8aac122bd4f6e的角平分线，

           6ec8aac122bd4f6e

           又6ec8aac122bd4f6e

           6ec8aac122bd4f6e      4分

       （II）连结DE，

           6ec8aac122bd4f6e⊙O切BC于D，

           6ec8aac122bd4f6e       5分

           由（I）可得6ec8aac122bd4f6e

           又6ec8aac122bd4f6e⊙O内接四边形AEDF，

           6ec8aac122bd4f6e∽6ec8aac122bd4f6e

           6ec8aac122bd4f6e分

           又6ec8aac122bd4f6e

           6ec8aac122bd4f6e       10分

    23．解：（I）把6ec8aac122bd4f6e化为普通方程为

           6ec8aac122bd4f6e      2分

           把6ec8aac122bd4f6e化为直角坐标系中的方程为

           6ec8aac122bd4f6e       4分

           6ec8aac122bd4f6e圆心到直线的距离为6ec8aac122bd4f6e       6分

       （II）由已知6ec8aac122bd4f6e       8分

           6ec8aac122bd4f6e

           6ec8aac122bd4f6e       10分

    24．证明：法一：6ec8aac122bd4f6e

           6ec8aac122bd4f6e     

           6ec8aac122bd4f6e  5分

           6ec8aac122bd4f6e

           6ec8aac122bd4f6e

           6ec8aac122bd4f6e        10

           法二：

           6ec8aac122bd4f6e

           6ec8aac122bd4f6e      5分

           6ec8aac122bd4f6e

        6ec8aac122bd4f6e        10分

     

    本资料由《七彩教育网》www.7caiedu.cn 提供！


    同步练习册答案