练习册

  • 练习册
  • 试题
    C．函数轴的交点的横坐标由小到大依次构成一个无穷等差数列 【查看更多】

     

    题目列表(包括答案和解析)

    设函数f（x）是定义在R上的偶函数，且f（x+2）=f（x）恒成立；当x∈[0，1]时，f（x）=x3-4x+3．有下列命题：
    ①f(-
    3
    4
    ) ＜f(
    15
    2
    )    ；
    ②当x∈[-1，0]时f（x）=x3+4x+3；
    ③f（x）（x≥0）的图象与x轴的交点的横坐标由小到大构成一个无穷等差数列；
    ④关于x的方程f（x）=|x|在x∈[-3，4]上有7个不同的根．
    其中真命题的个数为（　　）

    查看答案和解析>>

    设函数f（x）是定义在R上的偶函数，且f（x+2）=f（x）恒成立；当x∈[0，1]时，f（x）=x3-4x+3．有下列命题：
    ①；
    ②当x∈[-1，0]时f（x）=x3+4x+3；
    ③f（x）（x≥0）的图象与x轴的交点的横坐标由小到大构成一个无穷等差数列；
    ④关于x的方程f（x）=|x|在x∈[-3，4]上有7个不同的根．
    其中真命题的个数为（ ）
    A．1个
    B．2个
    C．3个
    D．4个

    查看答案和解析>>

    设函数f（x）是定义在R上的偶函数，且f（x+2）=f（x）恒成立；当x∈[0，1]时，f（x）=x3-4x+3．有下列命题：
    ①数学公式；
    ②当x∈[-1，0]时f（x）=x3+4x+3；
    ③f（x）（x≥0）的图象与x轴的交点的横坐标由小到大构成一个无穷等差数列；
    ④关于x的方程f（x）=|x|在x∈[-3，4]上有7个不同的根．
    其中真命题的个数为


    1. A.
      1个
    2. B.
      2个
    3. C.
      3个
    4. D.
      4个

    查看答案和解析>>

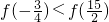    已知函数f(x)＝2cos2x＋2sinx cosx－1的图象与g(x)＝－1的图象在y轴的右侧交点按从横坐标由小到大的顺序记为D1，D2，D3，…，则＝

    [　　]

    A．π

    B．

    C．2π

    D．

    查看答案和解析>>

    已知函数f（x）=2cos2x+2sinxcosx-1的图象与g（x）=-1的图象在y轴的右侧交点按从横坐标由小到大的顺序记为D1，D2，D3，…，则|D5D7|=（　　）

    查看答案和解析>>

     

    第I卷（选择题 共60分）

    一、选择题（每小题5分，共60分）

    1―6ADDCAB  7―12CBBCBC

    第Ⅱ卷（非选择题 共90分）

    二、填空题（每小题4分，共16分）

    13．2  14．   15．  16．①②

    三、解答题（本大题共6小题，共74分）

    17．解：（I）

          

          

              4分

           又    2分

       （II）    

               2分

                 1分

          

          

                  3分

    18．（I）证明：由题意可知CD、CB、CE两两垂直。

           可建立如图所示的空间直角坐标系

           则       2分

           由  1分

          

           又平面BDF，

           平面BDF。       2分

       （Ⅱ）解：设异面直线CM与FD所成角的大小为

          

          

           。

           即异面直线CM与FD所成角的大小为   3分

       （III）解：平面ADF，

           平面ADF的法向量为      1分

           设平面BDF的法向量为

           由

                1分

          

              1分

           由图可知二面角A―DF―B的大小为   1分

    19．解：（I）设该小组中有n个女生，根据题意，得

          

           解得n=6,n=4（舍去）

           该小组中有6个女生。        6分

       （Ⅱ）由题意，甲、乙、丙3人中通过测试的人数不少于2人，

           即通过测试的人数为3人或2人。

           记甲、乙、丙通过测试分别为事件A、B、C，则

          

                6分

    20．解：（I）的等差中项，

                 1分

           。

                 2分

                    1分

       （Ⅱ）

                   2分

          

              3分

           ，   

           当且仅当时等号成立。

          

    21．解：（I）到渐近线=0的距离为，两条准线之间的距离为1，

                   3分

                1分

       （II）由题意，设

           由     1分

                3分

       （III）由双曲线和□ABCD的对称性，可知A与C、B与D关于原点对称。

           而   

           1分

           点O到直线的距离   1分

                  1分

                 1分

    22．解：（I）当t=1时,   1分

           当变化时，的变化情况如下表：

          

    （-1，1）

    1

    （1，2）

    ―

    0

    +

    极小值

           由上表，可知当    2分

                1分

       （Ⅱ）

          

           显然的根。    1分

           为使处取得极值，必须成立。

           即有    2分

          

           的个数是2。

       （III）当时，若恒成立，

           即   1分

          

           ①当时，

           ，

           上单调递增。

          

          

           解得    1分

           ②当时，令

           得（负值舍去）。

       （i）若时，

           上单调递减。

          

          

               1分

       （ii）若

           时，

           当

           上单调递增，

          

           要使，则

          

                2分

       （注：可证上恒为负数。）

           综上所述，t的取值范围是。        1分

     


    同步练习册答案