
题目列表(包括答案和解析)
、为调查某地中学生平均每人每天参加体育锻炼时间 (单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上.有10000名中学生参加了此项活动,下图是此次调查中某一项的流程图,其输出的结果是6200,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )
(单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上.有10000名中学生参加了此项活动,下图是此次调查中某一项的流程图,其输出的结果是6200,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )
A.0.62 B.0.38 C.6200 D.3800

、某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天100颗种子的发芽数,如下
|
日期 |
12月1日 |
12月2日 |
12月3日 |
12月4日 |
12月5日 |
|
温差 |
10 |
11 |
13 |
12 |
8 |
|
发芽数 |
23 |
25 |
30 |
26 |
16 |
该农科所确定的研究方案是:先从这五组数据中选取两组,用剩下的3组数据求线性回归方程,再用被选取点2组数据进行检验
(1)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求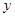 关于
关于 的线性回归方程
的线性回归方程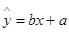 ;
;
(2)若线性回归方程得到的估计数据与所选点检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得到的线性回归方程是否可靠?
参考公式: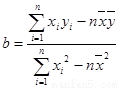 ,
,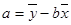
| A.11×(1.15-1)a亿元 | B.10×(1.15-1)a 亿元 |
| C.11×(1.14-1)a 亿元 | D.10×(1.14-1)a亿元 |
 (单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上.有10000名中学生参加了此项活动,下图是此次调查中某一项的流程图,其输出的结果是6200,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )
(单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上.有10000名中学生参加了此项活动,下图是此次调查中某一项的流程图,其输出的结果是6200,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )| A.0.62 | B.0.38 | C.6200 | D.3800 |

、某厂去年产值是a亿元,计划今后五年内年产值平均增长率是10%.则从今年起到第5年末的该厂总产值是 ( )
| A.11×(1.15-1)a亿元 | B.10×(1.15-1)a 亿元 |
| C.11×(1.14-1)a 亿元 | D.10×(1.14-1)a亿元 |
一、选择题(本大题8小题,共40分,每小题给出的四个选项中,只有一项是符合要求)
题号
1
2
3
4
5
6
7
8
答案
A
C
A
D
A
B
B
B
二、填空题:(本大题共须作6小题,每小题5分,共30分,把答案填写在题横线上).
9、 试题及答案.files/image134.gif) 10、
10、试题及答案.files/image136.gif) 11、
11、试题及答案.files/image138.gif) 12、3
12、3
▲选做题:在下面三道题中选做两题,三题都选的只计算前两题的得分。
13、3
;14、试题及答案.files/image140.gif) 。 ; 15、
。 ; 15、试题及答案.files/image142.gif)
三、解答题(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤)
16、(本小题满分14分)解:(1)试题及答案.files/image079.gif) 的内角和
的内角和试题及答案.files/image144.gif)
试题及答案.files/image146.gif)
试题及答案.files/image081.gif)
试题及答案.files/image148.gif) …………………1分
…………………1分
试题及答案.files/image150.gif)
试题及答案.files/image152.gif) ……………5分
……………5分
试题及答案.files/image154.gif)
试题及答案.files/image156.gif) …………………7分
…………………7分
(2)试题及答案.files/image158.gif)
试题及答案.files/image160.gif) ……………9分
……………9分
试题及答案.files/image162.gif)
试题及答案.files/image164.gif) …………12分
…………12分
当试题及答案.files/image166.gif) 即
即试题及答案.files/image168.gif) 时,y取得最大值
时,y取得最大值试题及答案.files/image170.gif) ………………………14分
………………………14分
17.(本小题满分12分)
解:(1)3个旅游团选择3条不同线路的概率为:P1=试题及答案.files/image172.gif) …………3分
…………3分
(2)恰有两条线路没有被选择的概率为:P2=试题及答案.files/image174.gif) ……6分
……6分
(3)设选择甲线路旅游团数为ξ,则ξ=0,1,2,3………………7分
P(ξ=0)=试题及答案.files/image176.gif) P(ξ=1)=
P(ξ=1)=试题及答案.files/image178.gif)
P(ξ=2)= 试题及答案.files/image180.gif) P(ξ=3)=
P(ξ=3)= 试题及答案.files/image182.gif) ………………9分
………………9分
∴ξ的分布列为:
ξ
0
1
2
3
试题及答案.files/image184.gif)
试题及答案.files/image184.gif)
试题及答案.files/image187.gif)
试题及答案.files/image189.gif)
………………10分
∴期望Eξ=0×试题及答案.files/image184.gif) +1×
+1×试题及答案.files/image184.gif) +2×
+2×试题及答案.files/image187.gif) +3×
+3×试题及答案.files/image189.gif) =
=试题及答案.files/image191.gif) ………………12分
………………12分
18.(本小题满分12分)
|