
题目列表(包括答案和解析)
(08年山东卷)(本小题满分12分)
将数列![]() 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
记表中的第一列数![]() 构成的数列为
构成的数列为![]() ,
,![]() .
.![]() 为数列
为数列![]() 的前
的前![]() 项和,且满足
项和,且满足![]() .
.
(Ⅰ)证明数列![]() 成等差数列,并求数列
成等差数列,并求数列![]() 的通项公式;
的通项公式;
(Ⅱ)上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当![]() 时,求上表中第
时,求上表中第![]() 行所有项的和.
行所有项的和.
每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,不能答在试题卷上。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.
1.设全集![]() ,
,![]()
![]() ,
,![]() ,则
,则![]() =
=
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.已知圆的方程为![]() ,那么下列直线中经过圆心的直线方程为
,那么下列直线中经过圆心的直线方程为
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
选择题每小题选出答案后,用2B铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,答在试题卷上无效。
(本小题满分14分)
将数列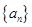 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表:
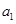
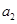
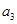
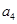
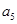
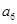
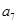
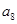
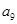
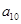
………………………
记表中的第一列数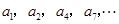 构成的数列为
构成的数列为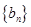 ,
,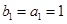 .
.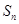 为数列
为数列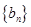 的前
的前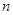 项和,且满足
项和,且满足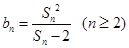 .
.
(1)证明: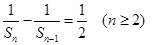 ;
;
(2)求数列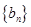 的通项公式;
的通项公式;
(3)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当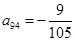 时,求上表中第
时,求上表中第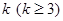 行所有项的和.
行所有项的和.
将数列![]() 中的所有项按每一行比上一行多一项的规则排成下表:
中的所有项按每一行比上一行多一项的规则排成下表:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
……
记表中的第一列数![]() 、
、![]() 、
、 ![]() 、
、 ![]() ……构成的数列为
……构成的数列为![]() ,
,![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,且满足
项和,且满足![]()
(I)证明数列![]() 成等差数列,并求数列
成等差数列,并求数列![]() 的通项公式;
的通项公式;
(II)上表中,若从第三行起,每一行中的数从左到右的顺序均构成等比数列,且公比为同一个正数,当![]() 时,求上表中第
时,求上表中第![]() 行所有项的和
行所有项的和
一、选择题
AACCD BBDDD AC
二、填空题
13. 14.6 15.①⑤ 16.
14.6 15.①⑤ 16.
三、解答题
17.解:(Ⅰ)因为 ,
,
由正弦定理,得 , ……3分
, ……3分
整理,得
因为 、
、 、
、 是
是 的三内角,所以
的三内角,所以 ,
,
因此  .
……6分
.
……6分
|