20080602
22.(18分) (1)ABD; (2)① 甲, ②150Ω ③E= .
.
评分标准:本题共18分.(1)问6分,选对但不全,每选一个给2分,有选错或不选得0分;(2)问共12分,①4分,②4分,③4分.
23.(15分)解:(1)(0~2)s内物体做匀减速直线运动,设加速度为a1,则有:
 -(F+f )= m a1
-(F+f )= m a1
(2~4)s内物体做匀加速直线运动,设加速度为a2,则有:a2=1m/s2
F―f = m a2
又f=μmg
所以解得,μ=0.2
(8分)
(2)由F―f = m a2 得
F= m a2 +f= m a2+μmg =150N (7分)
24.13、(20分)(1)ab棒做匀速直线运动,说明它受到的安培力与滑动摩擦力是一对平衡力,故有 : =
= 所以:
所以: (4分)
(4分)
 即:
即: (3分)
(3分)
 (3分)
(3分)
当ab棒匀速运动时,说明它所受到的安培力不变,也就是回路的感应电动势不变,此时cd棒也在做匀速运动,它受到的外力等于它受到的安培力和滑动摩擦力之和,由于ab棒和cd棒中的电流相同,长度相同,在同一磁场中,它们受到的安培力大小相等,方向相反,
所以:
作用在cd上的拉力F的功率为P, (2分)
(2分)
(2)当cd棒突然停止运动,而ab棒做切割磁感线的运动,所产生的感应电流在磁场中受到安培力(方向与刚才相反)和滑动摩擦力的共同作用使ab棒做减速运动,直到停止,此过程是一个加速度减小的减速运动,令△S是ab棒运动时扫过的面积, 是与此面积相对应ab棒滑动的距离.
是与此面积相对应ab棒滑动的距离.
则:

所以:
 (4分)
(4分)
此过程中克服摩擦力的功为 :
由能量守恒可知两金属棒上消耗的电能共为:
 (4分)
(4分)
25.(20分)解析:(1)点电荷 a 以水平向右的初速度v沿水平面进入匀强磁场恰好不脱离水平面。此时水平面对点电荷 a没有支持力,点电荷 a所受的重力和洛伦兹力相等。有:mg=qvB
B=mg/qv
(5分)
(2)点电荷 a 以水平向右的初速度v沿水平面进入匀强磁场恰好不脱离水平面, 以速度v沿水平面做匀速直线运动,进入匀强电场,也恰好不脱离水平面,此时水平面对点电 荷 a没有支持力,点电荷 a所受的重力和电场力相等。有:mg=qE
E=mg/q
(5分)
(3)点电荷a进入匀强电场后与小球b正碰并粘在一起,带正电电量为 q ,设共同速度为v1 ,由动量守恒定律得:

点电荷 a和小球一起恰好能绕悬挂点O在匀强电场中做竖直面内的圆周运动。它们通过最高点时,细线不受拉力作用。点电荷 a和小球受重力和电场力,设此时它们的速度为v2 ,由向心力公式得

 (3分)
(3分)
小球从最低点到最高点的过程中,由动能定理得



![]() +
+![]() →
→![]() +
+![]() +3x1 ②
+3x1 ②![]() +x2→
+x2→![]() +
+![]() ?
?![]() →
→![]() +x3 ④
+x3 ④![]() +
+![]() →
→![]() +x4?
+x4?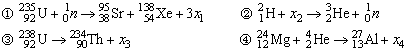
![]() 是中子 B.
是中子 B.![]() 是质子 C.
是质子 C.![]() 是α粒子 D.
是α粒子 D.![]() 是氘核
是氘核



![]()
![]()
![]()
![]()