
题目列表(包括答案和解析)
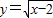 的定义域为集合M,集合N={y|y=x2,x∈M},则M∩N=( )
的定义域为集合M,集合N={y|y=x2,x∈M},则M∩N=( )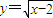 的定义域为集合M,集合N={y|y=x2,x∈M},则M∩N=( )
的定义域为集合M,集合N={y|y=x2,x∈M},则M∩N=( )设函数![]() 的定义域为集合M,集合N=
的定义域为集合M,集合N=![]() ,则M∩N=
,则M∩N=
A.M B.N C.[0,+∞) D.![]()
设函数![]() 的定义域为集合M,集合N={y|y=x2,x∈M},则M∩N=
的定义域为集合M,集合N={y|y=x2,x∈M},则M∩N=
A.M
B.N
C.[0,+∞)
D.![]()
设函数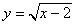 的定义域为集合M,集合
的定义域为集合M,集合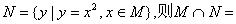 ( )
( )
A.M B.N C.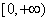 D.
D.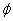
一、选择题:
题号
.files/image179.gif)
.files/image146.gif)
.files/image177.gif)
.files/image181.gif)
.files/image175.gif)
.files/image331.gif)
.files/image333.gif)
.files/image335.gif)
答案
.files/image337.gif)
.files/image339.gif)
.files/image341.gif)
.files/image343.gif)
.files/image341.gif)
.files/image339.gif)
.files/image343.gif)
.files/image337.gif)
1、解析:.files/image347.gif) ,N=
,N=.files/image349.gif) ,
,
即.files/image351.gif) .答案:
.答案:.files/image337.gif) .
.
2、解析:由题意得.files/image353.gif) ,又
,又.files/image355.gif) .
.
答案:.files/image339.gif) .
.
3、解析:程序的运行结果是.files/image357.gif) .答案:
.答案:.files/image341.gif) .
.
4、解析:与直线.files/image038.gif) 垂直的切线
垂直的切线.files/image036.gif) 的斜率必为4,而
的斜率必为4,而.files/image359.gif) ,所以,切点为
,所以,切点为.files/image361.gif) .切线为
.切线为.files/image363.gif) ,即
,即.files/image041.gif) ,答案:
,答案:.files/image343.gif) .
.
5、解析:由一元二次方程有实根的条件.files/image366.gif) ,而
,而.files/image368.gif) ,由几何概率得有实根的概率为
,由几何概率得有实根的概率为.files/image055.gif) .答案:
.答案:.files/image341.gif) .
.
6、解析:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面,所以.files/image343.gif) 正确;如果两个平面与同一条直线垂直,则这两个平面平行,所以
正确;如果两个平面与同一条直线垂直,则这两个平面平行,所以.files/image341.gif) 正确;
正确;
如果一个平面经过了另一个平面的一条垂线,则这两个平面平行,所以.files/image337.gif) 也正确;
也正确;
只有.files/image339.gif) 选项错误.答案:
选项错误.答案:.files/image339.gif) .
.
7、解析:由题意,得.files/image370.gif) ,答案:
,答案:.files/image343.gif) .
.
8、解析:.files/image142.gif) 的图象先向左平移
的图象先向左平移.files/image372.gif) ,横坐标变为原来的
,横坐标变为原来的.files/image146.gif) 倍
倍.files/image374.gif) .答案:
.答案:.files/image337.gif) .
.
二、填空题:
题号
.files/image376.gif)
.files/image378.gif)
.files/image380.gif)
.files/image382.gif)
.files/image384.gif)
.files/image386.gif)
.files/image388.gif)
答案
.files/image025.gif)
.files/image391.gif)
.files/image393.gif)
.files/image181.gif)
.files/image179.gif)
.files/image397.gif)
.files/image376.gif)
9、解析:若.files/image160.gif) ,则
,则.files/image400.gif) ,解得
,解得.files/image402.gif) .
.
10、解析:由题意.files/image404.gif) .
.
11、解析:.files/image406.gif)
.files/image408.gif)
12、解析:令.files/image410.gif) ,则
,则.files/image412.gif) ,令
,令.files/image414.gif) ,则
,则.files/image416.gif) ,
,
令.files/image418.gif) ,则
,则.files/image420.gif) ,令
,令.files/image422.gif) ,则
,则.files/image424.gif) ,
,
令.files/image426.gif) ,则
,则.files/image428.gif) ,令
,令.files/image430.gif) ,则
,则.files/image432.gif) ,
,
…,所以.files/image434.gif) .
.
13、解析:.files/image191.gif) :
:.files/image436.gif) ;则圆心坐标为
;则圆心坐标为.files/image438.gif) .
.
.files/image195.gif) :
:.files/image440.gif) 由点到直线的距离公式得圆心到直线的距离为
由点到直线的距离公式得圆心到直线的距离为.files/image442.gif) ,所以要求的最短距离为
,所以要求的最短距离为.files/image444.gif) .
.
14、解析:由柯西不等式.files/image446.gif) ,答案:
,答案:.files/image397.gif) .
.
15、解析:显然.files/image216.gif) 与
与.files/image220.gif) 为相似三角形,又
为相似三角形,又.files/image448.gif) ,所以
,所以.files/image220.gif) 的面积等于
的面积等于.files/image218.gif) .
.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16、解: (Ⅰ).files/image450.gif)
.files/image452.gif) , ……………………… 2分
, ……………………… 2分
∴.files/image454.gif) ,………………………………………………… 4分
,………………………………………………… 4分
解得.files/image456.gif) .………………………………………………………………… 6分
.………………………………………………………………… 6分
(Ⅱ)由.files/image236.gif) ,得:
,得:.files/image458.gif) , ……………………… 8分
, ……………………… 8分
∴.files/image460.gif) ………………………………… 10分
………………………………… 10分
∴.files/image462.gif) .…………………………………………………………… 12分
.…………………………………………………………… 12分
17、解:(1).files/image464.gif) … 2分
… 2分
则.files/image171.gif) 的最小正周期
的最小正周期.files/image466.gif) , …………………………………4分
, …………………………………4分
且当.files/image468.gif) 时
时.files/image171.gif) 单调递增.
单调递增.
即.files/image470.gif) 为
为.files/image171.gif) 的单调递增区间(写成开区间不扣分).………6分
的单调递增区间(写成开区间不扣分).………6分
(2)当.files/image242.gif) 时
时.files/image472.gif) ,当
,当.files/image474.gif) ,即
,即.files/image476.gif) 时
时.files/image478.gif) .
.
所以.files/image480.gif) . …………………………9分
. …………………………9分
.files/image482.gif) 为
为.files/image171.gif) 的对称轴. …………………12分
的对称轴. …………………12分
18、解:
(Ⅰ)解法一:“有放回摸两次,颜色不同”指“先白再黑”或“先黑再白”,
记“有放回摸球两次,两球恰好颜色不同”为事件.files/image343.gif) ,………………………2分
,………………………2分
∵“两球恰好颜色不同”共.files/image485.gif) 种可能,…………………………5分
种可能,…………………………5分
∴.files/image487.gif) . ……………………………………………………7分
. ……………………………………………………7分
解法二:“有放回摸取”可看作独立重复实验, …………………………2分
∵每次摸出一球得白球的概率为.files/image489.gif) .………………………………5分
.………………………………5分
∴“有放回摸两次,颜色不同”的概率为.files/image491.gif) . ……………………………7分
. ……………………………7分
(Ⅱ)设摸得白球的个数为.files/image493.gif) ,依题意得:
,依题意得:
.files/image495.gif) ,
,.files/image497.gif) ,
,.files/image499.gif) .…………10分
.…………10分
∴.files/image501.gif) ,……………………………………12分
,……………………………………12分
.files/image503.gif) .……………………14分
.……………………14分
19、(Ⅰ)证明: 连结.files/image505.gif) ,
,.files/image507.gif) 与
与.files/image505.gif) 交于点
交于点.files/image509.gif) ,连结
,连结.files/image511.gif) .………………………1分
.………………………1分
.files/image450.gif)
.files/image205.gif) 是菱形, ∴
是菱形, ∴.files/image509.gif) 是
是.files/image505.gif) 的中点. ………………………………………2分
的中点. ………………………………………2分
.files/image450.gif) 点
点.files/image264.gif) 为
为.files/image266.gif) 的中点, ∴
的中点, ∴.files/image515.gif) . …………………………………3分
. …………………………………3分
.files/image517.gif) 平面
平面.files/image519.gif) 平面
平面.files/image270.gif) , ∴
, ∴.files/image268.gif) 平面
平面.files/image270.gif) . ……………… 6分
. ……………… 6分
.files/image529.gif) (Ⅱ)解法一:
(Ⅱ)解法一:
.files/image450.gif)
.files/image260.gif) 平面
平面.files/image205.gif) ,
,.files/image532.gif) 平面
平面.files/image205.gif) ,∴
,∴ .files/image534.gif) .
.
.files/image536.gif) ,∴
,∴.files/image538.gif) . …………………………… 7分
. …………………………… 7分
.files/image450.gif)
.files/image205.gif) 是菱形, ∴
是菱形, ∴.files/image541.gif) .
.
.files/image543.gif) ,
,
∴.files/image545.gif) 平面
平面.files/image547.gif) . …………………………………………………………8分
. …………………………………………………………8分
作.files/image549.gif) ,垂足为
,垂足为.files/image551.gif) ,连接
,连接.files/image553.gif) ,则
,则.files/image555.gif) ,
,
所以.files/image557.gif) 为二面角
为二面角.files/image558.gif) 的平面角. ………………………………… 10分
的平面角. ………………………………… 10分
.files/image450.gif)
.files/image262.gif) ,∴
,∴.files/image561.gif) ,
,.files/image563.gif) .
.
在Rt△.files/image565.gif) 中,
中,.files/image567.gif) =
=.files/image569.gif)
.files/image571.gif) ,…………………………… 12分
,…………………………… 12分
∴.files/image573.gif) .…………………………… 13分
.…………………………… 13分
∴二面角.files/image272.gif) 的正切值是
的正切值是.files/image575.gif) . ………………………… 14分
. ………………………… 14分
解法二:如图,以点.files/image343.gif) 为坐标原点,线段
为坐标原点,线段.files/image578.gif) 的垂直平分线所在直线为
的垂直平分线所在直线为.files/image095.gif) 轴,
轴,.files/image581.gif) 所在直线为
所在直线为.files/image097.gif) 轴,
轴,.files/image584.gif) 所在直线为
所在直线为.files/image586.gif) 轴,建立空间直角坐标系,令
轴,建立空间直角坐标系,令.files/image588.gif) ,……………2分
,……………2分
则.files/image590.gif) ,
,.files/image592.gif) ,
,.files/image594.gif) .
.
.files/image598.gif) ∴
∴.files/image600.gif) . ……………4分
. ……………4分
设平面.files/image602.gif) 的一个法向量为
的一个法向量为.files/image604.gif)
.files/image606.gif) ,
,
由.files/image604.gif)
.files/image609.gif)
.files/image604.gif)
.files/image612.gif) ,得
,得.files/image614.gif) ,
,
令.files/image616.gif) ,则
,则.files/image618.gif) ,∴
,∴.files/image620.gif) . …………………7分
. …………………7分
.files/image450.gif)
.files/image260.gif) 平面
平面.files/image205.gif) ,
,.files/image532.gif) 平面
平面.files/image205.gif) ,
,
∴.files/image534.gif) . ………………………………… 8分
. ………………………………… 8分
.files/image536.gif) ,∴
,∴.files/image538.gif) .
.
.files/image450.gif)
.files/image205.gif) 是菱形,∴
是菱形,∴.files/image541.gif) .
.
.files/image543.gif) ,∴
,∴.files/image545.gif) 平面
平面.files/image270.gif) .…………………………… 9分
.…………………………… 9分
∴.files/image628.gif) 是平面
是平面.files/image270.gif) 的一个法向量,
的一个法向量,.files/image631.gif)
.files/image633.gif) .………………… 10分
.………………… 10分
∴.files/image635.gif) ,
,
∴.files/image637.gif) , …………………… 12分
, …………………… 12分
∴.files/image639.gif) .…………………………………… 13分
.…………………………………… 13分
∴二面角.files/image272.gif) 的正切值是
的正切值是.files/image575.gif) . ……………………… 14分
. ……………………… 14分
20、解:圆.files/image288.gif) 的方程为
的方程为.files/image642.gif) ,则其直径长
,则其直径长.files/image644.gif) ,圆心为
,圆心为.files/image646.gif) ,设
,设.files/image036.gif) 的方程为
的方程为.files/image649.gif) ,即
,即.files/image651.gif) ,代入抛物线方程得:
,代入抛物线方程得:.files/image653.gif) ,设
,设.files/image655.gif) ,
,
.files/image656.gif) 有
有.files/image658.gif) , ………………………………2分
, ………………………………2分
则.files/image660.gif) . ……………………4分
. ……………………4分
故.files/image662.gif) …6分
…6分
.files/image664.gif) , ………… 7分
, ………… 7分
因此.files/image666.gif) . ………………………………… 8分
. ………………………………… 8分
据等差,.files/image668.gif) , …………… 10分
, …………… 10分
所以.files/image670.gif) ,即
,即.files/image672.gif) ,
,.files/image674.gif) ,…………… 12分
,…………… 12分
即:.files/image036.gif) 方程为
方程为.files/image677.gif) 或
或.files/image679.gif) . …………………14分
. …………………14分
21、解:
(1)因为.files/image681.gif) , …………………………2分
, …………………………2分
所以.files/image683.gif) ,满足条件
,满足条件.files/image685.gif) . …………………3分
. …………………3分
又因为当.files/image687.gif) 时,
时,.files/image689.gif) ,所以方程
,所以方程.files/image313.gif) 有实数根
有实数根.files/image692.gif) .
.
所以函数.files/image303.gif) 是集合M中的元素. …………………………4分
是集合M中的元素. …………………………4分
(2)假设方程.files/image313.gif) 存在两个实数根
存在两个实数根.files/image695.gif) ),
),
则.files/image697.gif) ,……………………………………5分
,……………………………………5分
不妨设.files/image699.gif) ,根据题意存在数
,根据题意存在数.files/image701.gif)
使得等式.files/image703.gif) 成立, ………………………7分
成立, ………………………7分
因为.files/image705.gif) ,所以
,所以.files/image707.gif) ,与已知
,与已知.files/image301.gif) 矛盾,
矛盾,
所以方程.files/image313.gif) 只有一个实数根;………………………10分
只有一个实数根;………………………10分
(3)不妨设.files/image711.gif) ,因为
,因为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com