
题目列表(包括答案和解析)
C.选修4-4:坐标系与参数方程
在极坐标系下,已知圆O: 和直线
和直线 ,
,
(1)求圆O和直线 的直角坐标方程;(2)当
的直角坐标方程;(2)当 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
D.选修4-5:不等式证明选讲
对于任意实数
 和
和 ,不等式
,不等式 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
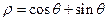 和直线
和直线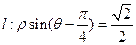 ,
, 的直角坐标方程;(2)当
的直角坐标方程;(2)当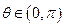 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.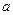
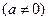 和
和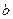 ,不等式
,不等式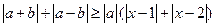 恒成立,试求实数
恒成立,试求实数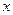 的取值范围.
的取值范围.C
[解析] 由基本不等式,得ab≤![]() =
=![]() =
=![]() -ab,所以ab≤
-ab,所以ab≤![]() ,故B错;
,故B错;![]() +
+![]() =
=![]() =
=![]() ≥4,故A错;由基本不等式得
≥4,故A错;由基本不等式得![]() ≤
≤![]() =
=![]() ,即
,即![]() +
+![]() ≤
≤![]() ,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×
,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×![]() =
=![]() ,故D错.故选C.
,故D错.故选C.
.定义域为R的函数 满足
满足 ,且当
,且当 时,
时, ,则当
,则当 时,
时, 的最小值为( )
的最小值为( )
(A) (B)
(B) (C)
(C) (D)
(D)
.过点 作圆
作圆 的弦,其中弦长为整数的共有 ( )
的弦,其中弦长为整数的共有 ( )
A.16条 B. 17条 C. 32条 D. 34条
一:选择题
题号
1
2
3
4
5
6
7
8
答案代号
C
A
A
C
C
B
A
B
二.填空题: 9 . 2 10、 11、
11、  ,
,
 12 . 60
12 . 60
13、 2 14、 (或
(或 ) , 两条直线 15、 16
) , 两条直线 15、 16
1.C;  ,
, 
2、A; 显然 为奇函数,且单调递增。于是
若
为奇函数,且单调递增。于是
若 ,则
,则 ,有
,有 ,即
,即 ,从而有
,从而有 .
.
反之,若 ,则
,则 ,推出
,推出
 ,即
,即
 。故选A。
。故选A。
3、A; 由 , 知
, 知  ;
;
4、C;  0
0
5、C; 
6、B; 
 ,
,  ;
;
7、A 把握住4,6,8三个面有一个共同的顶点这一个特点
 8、B; 如下图,设
8、B; 如下图,设 ,
, ,则
,则 .
.
由平行四边形法则,知NP∥AB,所以 =
= ,同理可得
,同理可得 .故
.故 ,选B.
,选B.
9、2(略)
10、60; 力F(x)所作的功为
11、 从图中看出
从图中看出  ,
,
所以选A



12、 ;
根据题中的信息,可以把左边的式子归纳为从
;
根据题中的信息,可以把左边的式子归纳为从 个球(n个白球,k个黑球)中取出m个球,可分为:没有黑球,一个黑球,……,k个黑球等
个球(n个白球,k个黑球)中取出m个球,可分为:没有黑球,一个黑球,……,k个黑球等 类,故有
类,故有 种取法。
种取法。
13、2; 由已知得  ,
,  ,
,
解得 
14、 ;两条直线;由
;两条直线;由 ,得
,得 ,
, ,
,
 ,
, ;两条直线
;两条直线
15、16;
由 可化为xy =8+x+y,
可化为xy =8+x+y, x,y均为正实数
x,y均为正实数
 xy =8+x+y
xy =8+x+y (当且仅当x=y等号成立)即xy-2
(当且仅当x=y等号成立)即xy-2 -8
-8
可解得
 ,即xy
,即xy 16故xy的最小值为16。
16故xy的最小值为16。
三、解答题:
16、(本小题满分12分)
解:
 ………………3分
………………3分
(Ⅰ)函数 的最小正周期
的最小正周期 ,
………………5分
,
………………5分
令 ,
,


∴函数 的单调递减区间为
的单调递减区间为 …………7分
…………7分
(Ⅱ)
---------------12分
17、(本小题满分14分)
解: 将一颗骰子先后抛掷2次,此问题中含有36个等可能基本事件-----------1分
(1)
记“两数之和为
所以P(A)= ;
;
答:两数之和为6的概率为 。--------------------------------------- 4分
。--------------------------------------- 4分
(2)记“两数之和是3的倍数”为事件B,则事件B中含有12个基本事件,
所以P(B)= ;
;
答:两数之和是3的倍数的概率为 。-------------------------------7分
。-------------------------------7分
(2) 记“向上的两数之积是6的倍数”为事件C,则事件C中含有其中的15个等可能基本事件,
所以P(C)= ,
,
答:两数之积是6的倍数的概率为 。-------------------------------10分
。-------------------------------10分
(3) 基本事件总数为36,点(x,y),在圆x2+y2=25的内部记为事件D,则D包含13个事件,
所以P(D)= 。
。
答:点(x,y)在圆x2+y2=25的内部的概率 。----------------------14分
。----------------------14分
18、(本小题满分13分)
解: , -----------------2分
, -----------------2分
因为函数 在
在 处的切线斜率为-3,
处的切线斜率为-3,
所以 ,即
,即 ,------------------------3分
,------------------------3分
又 得
得 。------------------------4分
。------------------------4分
(1)函数 在
在 时有极值,所以
时有极值,所以 ,-------5分
,-------5分
解得 ,------------------------------------------7分
,------------------------------------------7分
所以 .------------------------------------8分
.------------------------------------8分
(2)因为函数 在区间
在区间 上单调递增,所以导函数
上单调递增,所以导函数 在区间
在区间 上的值恒大于或等于零,------------------------------------10分
上的值恒大于或等于零,------------------------------------10分
则 得
得 ,
,
所以实数 的取值范围为
的取值范围为 .----------------------------------13分
.----------------------------------13分
19、(本小题满分13分)
 解(Ⅰ)在
解(Ⅰ)在 中,
中, ,
,
在 中,
中, ,
,
∵ ,
,
∴ .---------------------------2分
.---------------------------2分
∵平面 平面
平面 ,且交线为
,且交线为 ,
,
∴ 平面
平面 .
.
∵ 平面
平面 ,∴
,∴ .------------------------------------5分
.------------------------------------5分
(Ⅱ)设 与
与 相交于点
相交于点 ,由(Ⅰ)知
,由(Ⅰ)知 ,
,
∵ ,∴
,∴ 平面
平面 ,
,
∵ 平面
平面 ,∴平面
,∴平面 平面
平面 ,且交线为
,且交线为 ,---------7分
,---------7分
如图19-2,作 ,垂足为
,垂足为 ,则
,则 平面
平面 ,
,
连结 ,则
,则 是直线
是直线 与平面
与平面 所成的角.-------------------9分
所成的角.-------------------9分
由平面几何的知识可知 ,∴
,∴ .--------------11分
.--------------11分
在 中,
中, ,
,
在 中,
中, ,可求得
,可求得 .∴
.∴ .
.
------------------------------------------------------------------------13分
20、(本题满分14分)
【解析】(I)因为 边所在直线的方程为
边所在直线的方程为 ,且
,且 与
与 垂直,
垂直,
所以直线 的斜率为
的斜率为 .又因为点
.又因为点 在直线
在直线 上,
上,
所以 边所在直线的方程为
边所在直线的方程为 .
. .-----------------3分
.-----------------3分
(II)由 解得点
解得点 的坐标为
的坐标为 ,
------------4分
,
------------4分
因为矩形 两条对角线的交点为
两条对角线的交点为 .
.
所以 为矩形
为矩形 外接圆的圆心.
-----------------6分
外接圆的圆心.
-----------------6分
又 .
.
从而矩形 外接圆的方程为
外接圆的方程为 .----------------------9分
.----------------------9分
(III)因为动圆 过点
过点 ,所以
,所以 是该圆的半径,又因为动圆
是该圆的半径,又因为动圆 与圆
与圆 外切,
外切,
所以 ,即
,即 .------------------------11分
.------------------------11分
故点 的轨迹是以
的轨迹是以 为焦点,实轴长为
为焦点,实轴长为 的双曲线的左支.
的双曲线的左支.
因为实半轴长 ,半焦距
,半焦距 .
.
所以虚半轴长 .
.
从而动圆 的圆心的轨迹方程为
的圆心的轨迹方程为 .
-----------------14分
.
-----------------14分
21、(本小题满分14分)
解:(Ⅰ)由题意 即
即
∴ ……………………2分
……………………2分
∴ ∵m>0且
∵m>0且 ,∴m2为非零常数,
,∴m2为非零常数,
∴数列{an}是以m4为首项,m2为公比的等比数列 …………4分
(Ⅱ)由题意 ,
,
当
∴ ①
…………6分
①
…………6分
①式两端同乘以2,得
 ② …………7分
② …………7分
②-①并整理,得


=

 -----------------------------------------------10分
-----------------------------------------------10分
(Ⅲ)由题意

要使 对一切
对一切 成立,
成立,
即  对一切
对一切
 成立,
成立,
①当m>1时,  成立;
…………12分
成立;
…………12分
②当0<m<1时,
∴ 对一切
对一切
 成立,只需
成立,只需 ,
,
解得
 , 考虑到0<m<1, ∴0<m<
, 考虑到0<m<1, ∴0<m<
综上,当0<m< 或m>1时,数列{cn }中每一项恒小于它后面的项.
----------14分
或m>1时,数列{cn }中每一项恒小于它后面的项.
----------14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com