
题目列表(包括答案和解析)
等差数列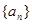 中,
中,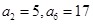 ,若数列
,若数列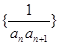 的前
的前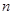 项和为
项和为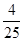 ,则
,则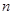 的值为
的值为
A、18 B、16 C、15 D、14
等差数列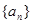 中,
中, ,若数列
,若数列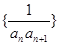 的前
的前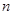 项和为
项和为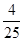 ,则
,则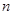 的值为
的值为
A、18 B、16 C、15 D、14
等差数列![]() 中,
中,![]() ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() 的值为
的值为
A、18 B、16 C、15 D、14
第Ⅱ卷(非选择题 共90分)
二. 填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
等差数列![]() 中,
中,![]() ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() 的值为
的值为
A、18 B、16 C、15 D、14
等差数列![]() 中,
中,![]() ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() 的值为( )
的值为( )
A、14 B、15 C、16 D、18
一、选择题: 1.B 2.B 3.D 4.C 5.C 6.C 7.D 8.A 9.C 10.B
二、填空题: 11. 12.
12. 13.
13. 14.
14. 15.1
15.1
三、解答题:
16.解: (Ⅰ)解: ,
, (1分)
(1分)
 (3分)
(3分)
 (4分)
(4分)

 (6分)
(6分)
(Ⅱ)解: (7分)
(7分)
由  得
得 (8分)
(8分)
由  得
得 (9分)
(9分)
 (11分)
(11分)
 (12分)
(12分)
17解: 设矩形温室的左侧边长为am,后侧边长为bm,则ab=800m2. (2分)
∴蔬菜的种植面积 , (5分)
, (5分)
∵ ,
,
∴ ,
(7分)
,
(7分)
∴ (m2),
(9分)
(m2),
(9分)
当且仅当 ,即
,即 时,
时, m2.
(11分)
m2.
(11分)
答:当矩形温室的左侧边长为40m,后侧边长为20m时,蔬菜的种植面积最大,最大种植面积为648 m2. (12分)
 18解:(Ⅰ)证明:
18解:(Ⅰ)证明:
 ,
,
∴ ,则
,则 (2分)
(2分)
又
 ,则
,则
∴ (4分)
(4分)
(Ⅱ)证明:依题意可知: 是
是 中点
中点

 则
则 ,而
,而
∴ 是
是 中点 (6分)
中点 (6分)
在 中,
中,
∴ (8分)
(8分)
(Ⅲ)解:

∴ ,而
,而
∴ ∴
∴ (10分)
(10分)

 是
是 中点
中点
∴ 是
是 中点 ∴
中点 ∴
 且
且


∴
∴ 中,
中,
∴ (12分)
(12分)
∴ (14分)
(14分)
19解: 圆C化成标准方程为: (2分)
(2分)
假设存在以AB为直径的圆M,圆心M的坐标为(a,b)
由于 ① (5分)
① (5分)
直线 的方程为
的方程为 (6分)
(6分)
 (7分)
(7分)

即: ② (10分)
② (10分)
由①②得: (11分)
(11分)
当 (12分)
(12分)
当 (13分)
(13分)
故这样的直线l 是存在的,方程为x-y+4=0或x-y+1=0. (14分)
20解: 解(Ⅰ) al0=10, a20=10+10d=40, ∴d=3 (2分)
(Ⅱ) a30= a20+10d=10(1+d+d2) (d≠0) (4分)
a30=10[(d+ )2+
)2+ ],
],
当d∈(-∞,
0)∪(0, +∞)时,
a30∈[ ,+∞].
(7分)
,+∞].
(7分)
(Ⅲ) 续写数列: 数列a30,a31,…,a40是公差为d4的等差数列 (8分)
一般地,可推广为:无穷数列{ an},其中al,a2…,a10是首项为1公差为1的等差数列,
当n≥1时, 数列a10n,a10n+1,…,a10(n+1)是公差为dn的等差数列. (9分)
研究的问题可以是:试写出a10(n+1)关于d的关系式,并求a10(n+1)的取值范围 (11分)
研究的结论可以是: 由a40= a30+10d3=10(1+d+d2+ d3),
 依次类推可得
a10(n+1)= 10(1+d+d2+…+ dn)= 10?
依次类推可得
a10(n+1)= 10(1+d+d2+…+ dn)= 10? (d≠1),
(d≠1),
10(n+1) (d=1)
当d>0时, a10(n+1)的取值范围为(10, +∞)等 (14分)
21解:(Ⅰ)由 过点P且以P(1,-2)为切点的直线的斜率
过点P且以P(1,-2)为切点的直线的斜率 ,
,
 所求直线方程:
所求直线方程: (3分)
(3分)
(Ⅱ)设过P(1,-2)的直线l与 切于另一点
切于另一点
知:
即:
或 故所求直线的斜率为:
故所求直线的斜率为:

即 (8分)
(8分)
(Ⅲ)由(Ⅱ)可知 则
则

在 上单调递增, (11分)
上单调递增, (11分)
在
得
 为两极值点,在
为两极值点,在 时,
时,
 上单调递增,
上单调递增,
即
 (14分)
(14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com