2．用轻质细线把两个质量未知的小球悬挂起来，如右图所示。今对小球a持续施加一个向左偏下30°大小为F的恒力，并对小球b持续施加一个向右偏上30°的大小为1.5F的恒力，最后达到平衡。表示平衡状态的图可能是

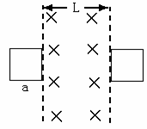1．如图所示，在光滑的水平面上，有竖直向下的匀强磁场，分布在宽度为L的区域里。现有一边长为a（a＜L的正方形闭合线圈刚好能穿过磁场，则线圈在滑进磁场过程中产生的热量Q₁与滑出磁场过程中产生的热量Q₂之比为

A．1：1

B．2：1

C．3：1

D．4：1

       （可能用到的数据：银河系的质量约为M=31×10⁴¹kg，原子质量单位 1u=1.66×10^―27kg，1u相当于1.5×10^―10J的能量，电子质量m=0.0005u，氦核质量m_a=4.0026u，氢核质量m_p=1.0087u，中微子v₀质量为零。

   （2）研究表明，银河系的年龄约为t=3.8×10¹⁷s，每秒银河系产生的能量约为1×10³⁷J（P=1×10³⁷J/s），现假定该能量全部来自上述氢核聚变反应，试估算银河系中氦的含量（最后结果保留一位有效数字）

   （3）根据你的估算结果，对银河系中氦的主要生成途径作出判断。

   （1）把氢核聚变就简化4个氢核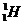（）聚变成氦核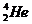（），同时放出2个正电子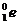（）和2个中微子（v₀），请写出该氢核聚变反应的方程，并计算一次反应释放的能量。

18．.(20分)天文学家测得银河系中氦的含量约为5%。有关研究表明，宇宙中氦生成的途径有两条：一是在宇宙诞生后2分钟左右生成的；二是在宇宙演化到恒星诞生后，由恒生内部的氢核聚变反应生成的。

16．（16分）2005年10月12日9时，神舟六号载人飞船在酒泉卫星发射中心发射升空，在环绕地球飞行5天后，其返回舱于10月17日按照预定计划返回预定地区．神舟六号载人航天飞行的圆满成功，标志着我国在发展载人航天技术方面取得了又一个具有里程碑意义的重大胜利．（已知地球半径为R，地球表面的重力加速度为g），神舟六号载人飞船在离地面高度为H的圆轨道上运行的时间为t．求在这段时间内它绕行地球多少圈？