
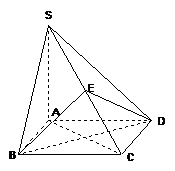
可求得点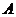 到平面
到平面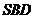 的距离为
的距离为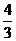
点评:求点到面的距离,经常采用等体积法,利用同一个几何体,体积相等,体现了转化思想.
(2)解:因为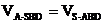 ,且
,且 ,
,
 平面
平面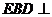 平面
平面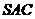
且

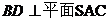
 (1)证明:
(1)证明: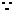
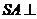 底面
底面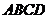
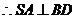
例题12.
由AF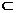 面PAD,则EF//面PAD.
面PAD,则EF//面PAD.
点评:证明面面垂直,先证明线面垂直,要证线面垂直,先证明线线垂直.
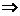 平面PDC
平面PDC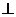 平面PAD;
平面PAD;
(2)取PD中点为F,连结EF、AF,由E为PC中点,
得EF为△PDC的中位线,则EF//CD,CD=2EF.
又CD=2AB,则EF=AB.由AB//CD,则EF∥AB.
所以四边形ABEF为平行四边形,则EF//AF.
证明:(1)由PA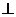 平面ABCD
平面ABCD

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com