设n为正整数，规定：f_n(x)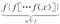＝，已知f(x)＝ .

(1)解不等式f(x)≤x；

(2)设集合A＝{0,1,2}，对任意x∈A，证明f₃(x)＝x；

(3)求f₂₀₀₇()的值；

(4)(理)若集合B＝，证明B中至少包含8个元素.

22.(本小题满分12分)

　　 (文)已知函数f(x)＝－x³＋ax²＋bx＋c图像上的点P(1，－2)处的切线方程为y＝－3x＋1.

(1)若函数f(x)在x＝－2时有极值，求f(x)的表达式；

(2)函数f(x)在区间[－2,0]上单调递增，求实数b的取值范围.

21.(本小题满分12分)

　　(理)已知实数a为整数.函数f(x)＝x³－2ax²－3a²x在区间(－1,1)上有极大值，在区间(1，＋∞)上有极小值，函数g(x)＝ax³＋(a＋b)x²－b，若g(x)≥f(x)在区间[－1,2]恒成立.

(1)求实数a的值；

(2)求实数b的取值范围.

(1)若年销售量增加的比例为0.4x，为使本年度的年利润比上年度有所增加，则投入成本增加的比例x应在什么范围内？

(2)年销售量关于x的函数为y＝3240(－x²＋2x＋)，则当x为何值时，本年度的年利润最大？最大利润为多少？

　　(文)某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆，出厂价为13万元/辆，年销售量为5000辆.本年度为适应市场需求，计划提高产品档次，适当增加投入成本，若每辆车投入成本增加的比例为x(0＜x＜1)，则出厂价相应提高的比例为0.7x，年销售量也相应增加.已知年利润＝(每辆车的出厂价－每辆车的投入成本)×年销售量.

(2)求 .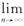

20.(本小题满分12分)

　　(理)已知函数f(x)＝－(x≤－1)，数列{a_n}中，a₁＝－1，a_n＝f^－1(a_n－1)(n＝2,3,4，…).

(1)求a_n，并加以证明；

19.(本小题满分12分)

　　(理)有A、B、C、D四个城市，它们都有一个著名的旅游点，依次记为a，b，c，d，把A、B、C、D和a，b，c，d分别写成左右两列，现在一名旅游爱好者随机用4条线把左右两边的字母全部连接起来，构成“一一对应”.已知每连对一个得2分，连错得0分.

(1)求该爱好者得分的分布列； 

(2)求该爱好者得分的数学期望.

　　(文)已知7件产品中有4件正品和3件次品.

(1)从这7件产品中一次性随机抽出3件，求抽出的产品中恰有1件正品数的概率；

(2)从这7件产品中一次性随机抽出4件，求抽出的产品中正品件数不少于次品件数的概率.

18.(本小题满分12分)

已知f(x)＝－3x²＋a(6－a)x＋b.

(1)解关于a的不等式f(1)>0；

(2)当不等式f(x)>0的解集为(?1,3)时，求实数a，b的值.