1. (10分)有一拦水坝是等腰楼形,它的上底是6米,下底是10米,高为2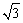米,求此拦水坝斜坡的坡度和坡角.

1.4　 船有触礁的危险吗

2.实习作业：测量小河对岸工厂烟囱的高，请用测量工具测量各数据并填入下表，完成下列实习报告.

测量 目标	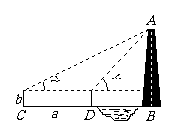测量底部不可到达的建筑物的高
测 量 示 意 图
测 量 程 序	测量项目	第一次	第二次	平均值
CD的长
测倾器的高
倾角α
倾角β
计算	烟囱AB的高(精确到0.1 m)

[综合练习]

如图1-22，A、B是两幢地平高度相等，隔岸相望的建筑物，B楼不能到达. 由于建筑物密集，在A楼的周围没有开阔地带，要测量B楼的高度只能充分利用A楼的空间. A楼的各层都可到达且能看见B楼，仅有的工具只是皮尺和测角器.

(1)请你设计一个测量B楼高度的方法，写出

测量步骤和必需的测量数据(用字母表示)，

并画出测量图形；

(2)用你测量的数据(用字母表示)，写出计算

B楼高度的表达式.

练习二

[基础练习]略

[综合练习]方法一(1)如图7-1，设用AC表示A楼，BD表示B楼，测量步骤如下：

① 用测角器在A楼的底部C处测出B楼顶部B的仰角为α；

② 用测角器在A楼的顶部A处测出B楼顶部B的仰角为β；

③ 用皮尺从A楼的顶部A处放下，测出A楼的高度为a.

(2)BD =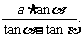

方法二 (1)如图7-2,设用AC表示A楼，BD表示B楼，测量步骤如下：

① 用测角器在A楼的顶部A处测出B楼底部D的俯角为α；

② 用测角器在A楼的顶部A处测出B楼顶部B的仰角为β；

③ 用皮尺从A楼的顶部A处放下，测出A楼的高度为a.　　　　　　　　　　

(2)BD = a (1 + ).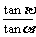

1.实习作业：测量学校教学大楼的高，请用测量工具测量各数据并填入下表，完成下列实习报告：

测量目标	测量底部可以到达的建筑物高
测 量 示 意 图
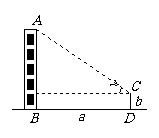测 量 程 序	测量项目	测量数据	计算高AB(精确到0.1米)
BD的长
测倾器的高
倾斜角

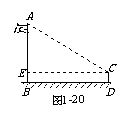如图1-20，光明中学九年级(2)班的同学用自己制作的侧倾器测量该校旗杆的高度，已知测倾器CD的高度为1.54米，测点D到旗杆的水平距离BD = 20米，测得旗杆顶A的仰角α= 35°，求旗杆AB的高度(精确到0.01米).

[综合练习]

如图1-21，小山上有一座铁塔AB，在山脚D处测得点A的仰角为60°，测得点B的仰角为45°，在E处测得点A的仰角为30°(C、D、E在同一条直线上)，并测得DE = 90 m，求小山BC和铁塔AB的高(精确到0.1 m).

5. 测量物体的高度

练习一

[基础练习]一、1. 80； 2. 7 +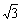. 二、1. A； 2. D. 三、15.54米.

[综合练习] 小山BC高45 m，铁塔AB高约32.9米.

2.如图1-19，两建筑物的水平距离为a米，从A点测得D点的俯角为α，测得C点的俯角为β. 则较低建筑物CD的高度为(　　 ).

A. a米　　　　 B. 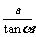　　　　　C. 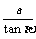　　　　　D. a (tanβ- tanα)

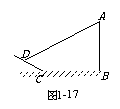
1.如图1-18，测量人员在山脚A处测得山顶B的仰角为45°，沿着倾角为30°的山坡前进1 000米到达D处，在D处测得山顶B的仰角为60°，则山高BC大约是(精确到0.01米)(　　 )；

A. 1 366.00米　　 B. 1 482.12米　　 C. 1 295.93米　　 D. 1 508.21米

2.如图1-17，小明想测量电线杆AB的高度，发现电线杆的影子恰好落在地面BC和斜坡的坡面CD上，测得BC = 10米，CD = 4米，CD与地面成30°角，且此时测得1米杆的影长为2米，则电线杆的高度为 　　　　　米.

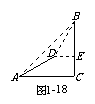
1.如图1-16，在高20米的建筑物CD的顶部C测得塔顶A的仰角为60°，测得塔底B的俯角为30°，则塔高AB = 　　　米；

4.如图，在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于D.

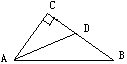
(1)若BC=8，BD=5，则点D到AB的距离是　　　　　 .

(2)若BD：DC=3：2，点D到AB的距离为6，则BC的长是　　　　　 .

理由：